Developing a sense for colliders
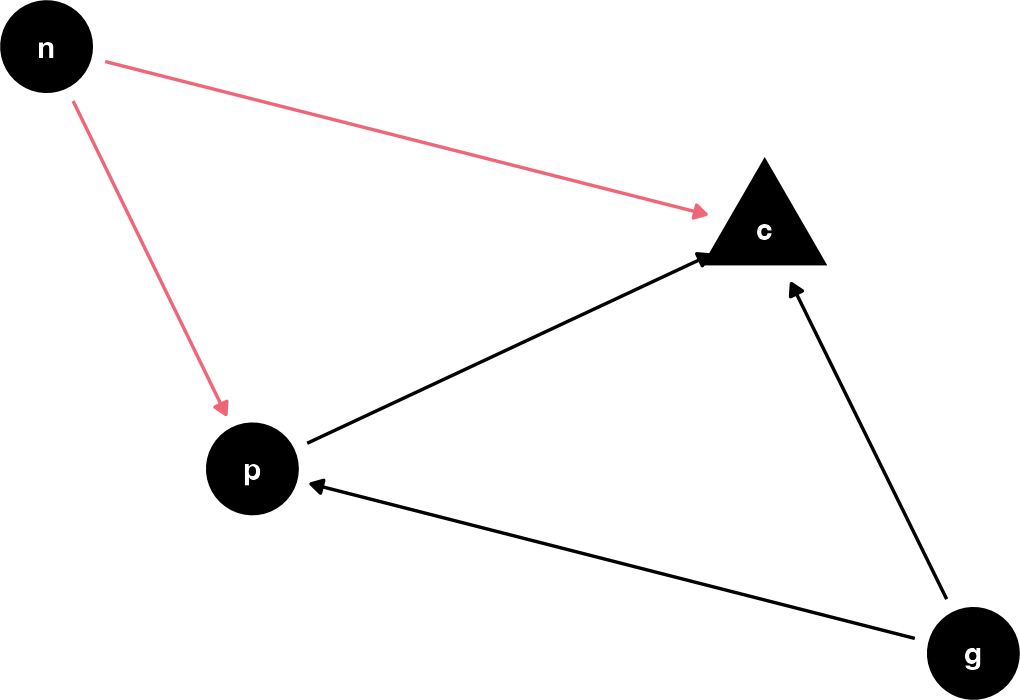
For me to really get a sense of how coliders work, I’m going to have to simulate a few different datasets, messing around with the parameters, and compare the outcomes. I won’t do this full Bayesian for the sake of speed. As a reminder, here’s the DAG. I’ll specifically be messing around with the effect of n on p and c.
Code
dagify (~ p + g + n,~ g + n|> tidy_dagitty () -> |> mutate (from_n = ifelse (name == "n" , ptol_red, "black" )|> ggplot (aes (x = x, y = y, xend = xend, yend = yend)) + geom_dag_point (aes (shape = name == "c" + geom_dag_edges (aes (edge_color = from_n+ geom_dag_text ()+ scale_color_manual (values = c ("grey60" , ptol_red)+ guides (shape = "none" ,color = "none" + theme_dag ()
Figure 1: DAG with a collider
I refactored the code from before into a function:
simulation function
<- function (n = 200 ,# Grandparent on parent b_GP = 1 ,# Parent on Child b_PC = b_GP,# Grandparent on Child b_GC = 0 ,# neighborhood b_N = 2 ){tibble (grandparent = rnorm (n),neighborhood = rbinom (size = 1 , prob = 0.5 parent = rnorm (mean = b_GP * grandparent + * neighborhoodchild = rnorm (mean = b_GC * grandparent + * parent + * neighborhood-> return (haunted_sim)
And I’ll do a grid of 100 values from -11 to 11 for b_N.
tibble (n = 200 ,b_GP = 1 ,b_PC = 1 ,b_GC = 0 ,b_N = rep (seq (- 11 , 11 , length = 100 ), 10 )->
Now, with some tidyverse fanciness, I’ll map the simulation function I wrote across each row to get simulation datasets.
Simulating the data with pmap
|> rowwise () |> mutate (data = pmap (list (n, b_GP, b_PC, b_GC, b_N),|> ungroup ()->
Then, for each data set I’ll fit
lm(child ~ parent + grandparent)and then get the parameters.
Fitting a model for each simulation
|> mutate (model = map (~ lm (child ~ parent + grandparent, data = .x)params = map (model, broom:: tidy)|> unnest (params) |> select (starts_with ("b_" ),->
Code
<- tibble (term = c ("(Intercept)" , "grandparent" , "parent" ),estimate = c (0 , 0 , 1 )|> ggplot (aes (+ geom_hline (data = true_params,aes (yintercept = estimatecolor = "grey40" + stat_summary (fun.y = mean,geom = "line" + facet_wrap (~ term)+ labs (caption = "b_GC = 0; b_GP = 1; b_PC = 1"
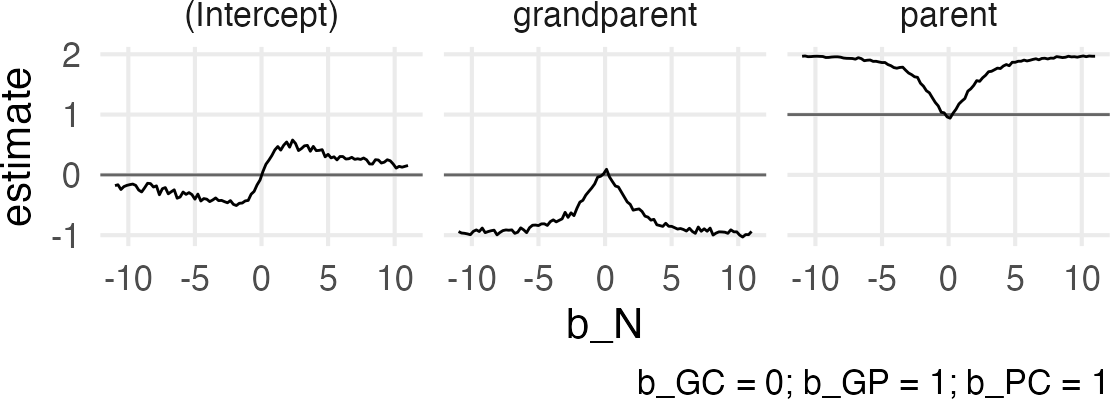
Figure 2: Collider effect
Huh. I guess I wasn’t expecting an asymptotic relationship for the grandparent and parent effects? It looks like as b_N gets large, the collider confounding reaches some kind of min/max, which for grandparent is -1, and for parent is 1. I don’t know if this value relates to either the effect of b_GP or b_PC, since both were set to 1? Maybe time for another grid search. I’ll really max outt the b_N effect to get fully into the tail of the asymptote.
expand_grid (n = 200 ,b_GP = rep (- 2 : 2 , 10 ),b_PC = rep (- 2 : 2 , 10 ),b_GC = 0 ,b_N = 50 |> rowwise () |> mutate (data = pmap (list (n, b_GP, b_PC, b_GC, b_N),|> ungroup () |> mutate (model = map (~ lm (child ~ parent + grandparent, data = .x)params = map (model, broom:: tidy)|> unnest (params) |> select (starts_with ("b_" ),->
Code
|> filter (!= "(Intercept)" |> ggplot (aes (+ stat_summary (fun.y = mean,geom = "line" + scale_x_continuous (breaks = c (- 2 , 0 , 2 )+ scale_y_continuous (breaks = c (- 2 , 0 , 2 )+ facet_grid (term~ b_PC, labeller = label_both)+ theme (aspect.ratio = 1 ,strip.text.y = element_text (size = 8 )+ labs (caption = "b_GC = 0; b_N = 50"
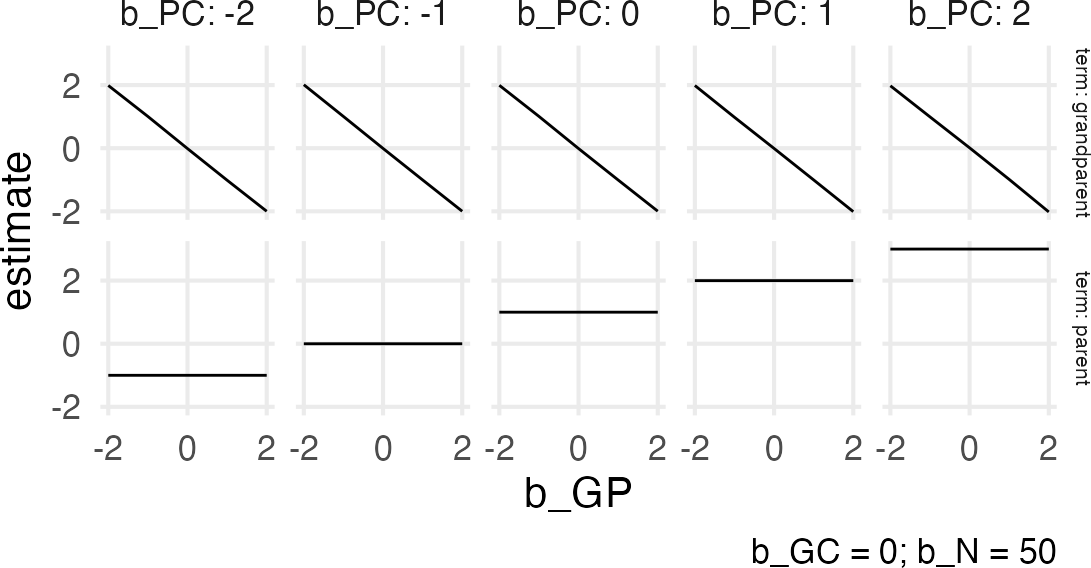
Figure 3: Collider effect
Huh. The associations look straightforward, but I think I need an animation to get it.
This turned into a whole thing.
Code
library (gganimate)= 100
Code
<- function (x, min.v = - 2 , max.v = 2 , scale = color ("berlin" )(100 )){= (x - min.v)/ (max.v- min.v)= round (prop * (length (scale)- 1 ))+ 1 return (scale[closest_idx])
Code
tibble (name = "p" ,to = "c" ,true = 1 ,est = true + 1 ,id = seq (- 2 , 2 , length = nframes),col = color_value (true)|> bind_rows (tibble (name = "g" ,to = "c" ,true = 0 ,est = seq (2 , - 2 , length = nframes),id = seq (- 2 , 2 , length = nframes),col = color_value (true)|> bind_rows (tibble (name = "g" ,to = "p" ,true = seq (- 2 , 2 , length = nframes),est = NA ,id = seq (- 2 , 2 , length = nframes),col = color_value (true)|> bind_rows (tribble (~ name, ~ to, ~ true, ~ est,"n" , "c" , NA , NA ,"n" , "p" , NA , NA ,"c" , NA , NA , NA |> mutate (across (true: est, as.numeric),col = "#000000" |> group_by (name, to, true, est, col) |> reframe (id = seq (- 2 , 2 , length = nframes)-> tibble (name = "p" ,to = "c" ,true = 1 ,est = true + 1 ,id = seq (- 2 , 2 , length = nframes),col = color_value (est)|> bind_rows (tibble (name = "g" ,to = "c" ,true = 0 ,est = seq (2 , - 2 , length = nframes),id = seq (- 2 , 2 , length = nframes),col = color_value (est)->
Code
|> left_join (the_dag |> as_tibble ()) -> |> left_join (the_dag |> as_tibble ()) ->
Code
|> ggplot (aes (x = x, y = y, xend = xend, yend = yend)) + geom_dag_point (color = "grey" ,+ geom_dag_text ()+ geom_segment (arrow = arrow (type = "closed" , length = unit (0.2 , "cm" )),linewidth = 1 ,aes (color = col+ geom_segment (data = est_dag,linetype = "dashed" ,aes (x = x+0.1 , y = y+0.1 , xend = xend+0.1 , yend = yend+0.1 ,color = colarrow = arrow (type = "closed" , length = unit (0.2 , "cm" )),linewidth = 1 + scale_color_identity ()+ transition_time (+ labs (title = "b_GP: {round(frame_time, digits = 2)} \n est_GC: {round(frame_time*-1, digits = 2)}" + theme_dag ()-> aanimate (a, rewind = T) |> anim_save (filename = "dag_anim.gif"
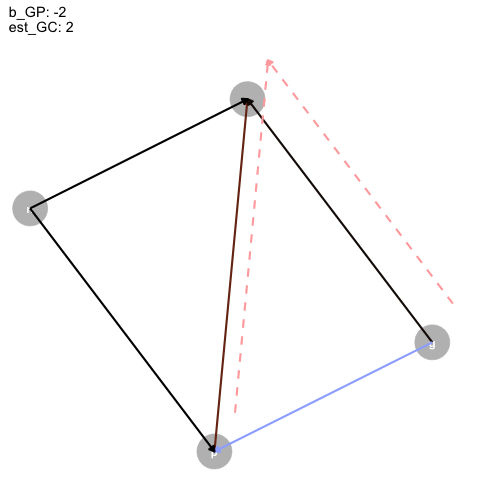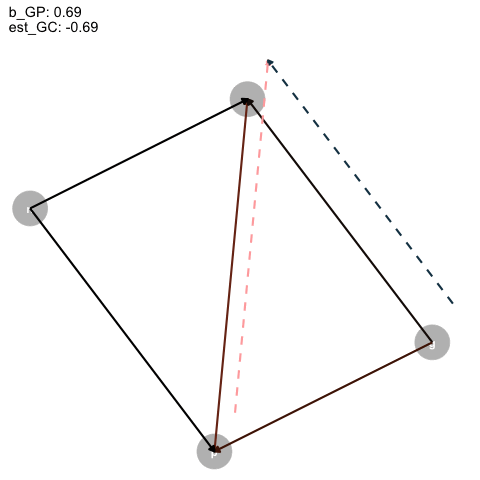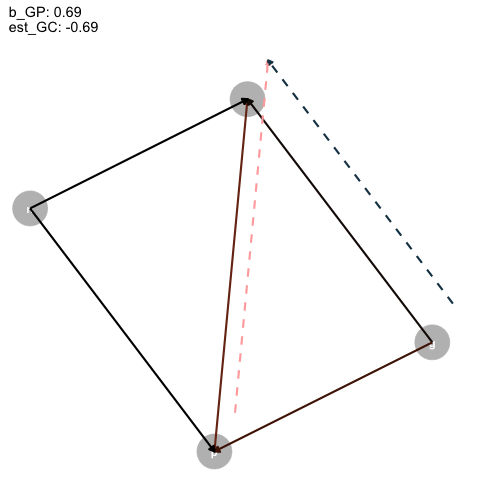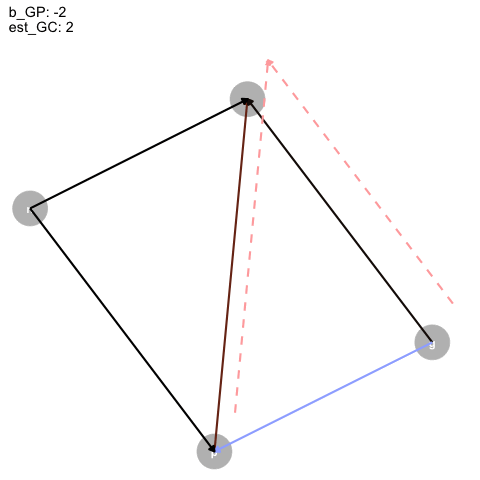
Figure 4: Animated DAG
So, as the true effect of Grandparents on parents changes, the estimated direct effect on children is inversely proportional, and, for some reason, the direct effect of parents is just +1?