Garden of Forking paths part 2

Author

Josef Fruehwald

Published

May 10, 2023

Modified

May 12, 2023

Listening 
renv::install("khroma")
library(tidyverse)
library(khroma)
library(gt)
library(patchwork)
library(here)
source(here("_defaults.R"))

A nicer table version.

I’d like to re-represent the Bayesian Update in a nicer GT table. Some options are

  1. Plotting extensions from {gtExtras}
  2. Emojis
renv::install("gtExtras")
renv::install("svglite")
renv::install("emoji")
library(gtExtras)
library(emoji)

First, trying the “win/losses” column plot from {gtExtra} to illustrate the blue vs white marbles.

tibble(
  blue_marbs = 0:4,
  white_marbs = 4 - blue_marbs
) |> 
  rowwise() |> 
  mutate(
    marbles = list(c(rep(1, blue_marbs), 
                     rep(0, white_marbs)))
  ) -> 
  marbles_wl

The cell background will have to be off-white for the white ticks to show

marbles_wl |> 
  gt() |> 
  gt_plt_winloss(marbles, palette = c("blue", "white", "grey")) |> 
  tab_style(style = cell_fill(color = "antiquewhite"), 
            locations = cells_body())
blue_marbs white_marbs marbles
0 4
1 3
2 2
3 1
4 0
Table 1:

Representing marble compositions with ‘win-loss’ plots

I’m not overwhelmed by the result. I’ll try emojis instead.

blue_marb <- emojis |> 
  filter(str_detect(name, "blue"), 
         str_detect(name, "circle")) |> 
  pull(emoji)

blue_marb
[1] "🔵"
white_marb <- emojis |> 
  filter(str_detect(name, "white"), 
         str_detect(name, "circle")) |> 
  pull(emoji)

white_marb
[1] "⚪"
tibble(
  blue_marbs = 0:4,
  white_marbs = 4 - blue_marbs
) |> 
  rowwise() |> 
  mutate(
    marbles = list(c(rep(blue_marb, blue_marbs), 
                     rep(white_marb, white_marbs)))
  ) -> 
  marbles_emoji
marbles_emoji |> 
  gt()
blue_marbs white_marbs marbles
0 4 ⚪, ⚪, ⚪, ⚪
1 3 🔵, ⚪, ⚪, ⚪
2 2 🔵, 🔵, ⚪, ⚪
3 1 🔵, 🔵, 🔵, ⚪
4 0 🔵, 🔵, 🔵, 🔵
Table 2:

Representing marble compositions with emoji

Update: As it turns out, getting tables with emoji and the plots with gt_plt_*() do not play nice with LaTeX. For now, I’m saving the tables to png with gtsave() just for the pdf output.

Yes, this is it.

Rerunning the sampling

I’ll re-run the sampling from the previous post.

sampling_df <- function(marbles, 
                        n = 1000, 
                        size = 3, 
                        pattern = c(blue_marb, white_marb, blue_marb)){
  sampling_tibble <- tibble(samp = 1:n)   
  sampling_tibble |> 
    mutate(
      chosen = map(samp, 
                   ~sample(marbles, 
                           size = 3, 
                           replace = T)),
      match = map_lgl(chosen, 
                      ~all(.x == pattern))                 
    ) |> 
    summarise(prop_match = mean(match))->                         
    sampling_tibble
  return(sampling_tibble)
}
marbles_emoji |> 
 ungroup() |> 
  mutate(
    prob = map(marbles, ~sampling_df(.x, n = 10000))
  ) |> 
  unnest(prob) |> 
  mutate(norm_probs = prop_match/sum(prop_match))->
  marble_probs

I want to label the column of probabilities with the key sequence.

key_seq <- str_glue("{blue_marb}, {white_marb}, {blue_marb}")

gtExtras::gt_plt_bar_pct() will plot a bar chart within the table.

marble_probs |> 
  select(marbles, norm_probs) |> 
  mutate(norm_probs = norm_probs * 100) |> 
  gt() |> 
  cols_label(
    norm_probs = str_glue("p(marbles | {key_seq})")
  ) |> 
  gt_plt_bar_pct(norm_probs, 
                 scaled = T, 
                 fill = "steelblue")
marbles p(marbles | 🔵, ⚪, 🔵)
⚪, ⚪, ⚪, ⚪
🔵, ⚪, ⚪, ⚪
🔵, 🔵, ⚪, ⚪
🔵, 🔵, 🔵, ⚪
🔵, 🔵, 🔵, 🔵
Table 3:

Probability of each marble composition given (🔵, ⚪️, 🔵) samples with replacement.

There we go!

With the Bayesian Update

marble_probs |> 
  mutate(new_prob = blue_marbs/sum(blue_marbs),
         multiplied = norm_probs * new_prob,
         norm_new = multiplied/sum(multiplied)) |> 
  select(marbles, norm_probs, norm_new) |> 
  mutate(norm_probs = norm_probs * 100,
         norm_new = norm_new * 100) |> 
  gt() |> 
  cols_label(
    norm_probs = str_glue("p(marbles | {key_seq})"),
    norm_new = str_glue("after {blue_marb}")
  ) |> 
  gt_plt_bar_pct(norm_probs, 
                 scaled = T, 
                 fill = "steelblue") |> 
  gt_plt_bar_pct(norm_new, 
                 scaled = T, 
                 fill = "steelblue") |> 
  cols_width(2 ~ px(200),
             3 ~ px(200))
marbles p(marbles | 🔵, ⚪, 🔵) after 🔵
⚪, ⚪, ⚪, ⚪
🔵, ⚪, ⚪, ⚪
🔵, 🔵, ⚪, ⚪
🔵, 🔵, 🔵, ⚪
🔵, 🔵, 🔵, 🔵
Table 4:

Probability of each marble composition given an additional (🔵) sample

Bayesian Updating

I’ll try to illustrate Baysian updating with an animated plotly plot.

renv::install("plotly")
renv::install("slider")
library(plotly)
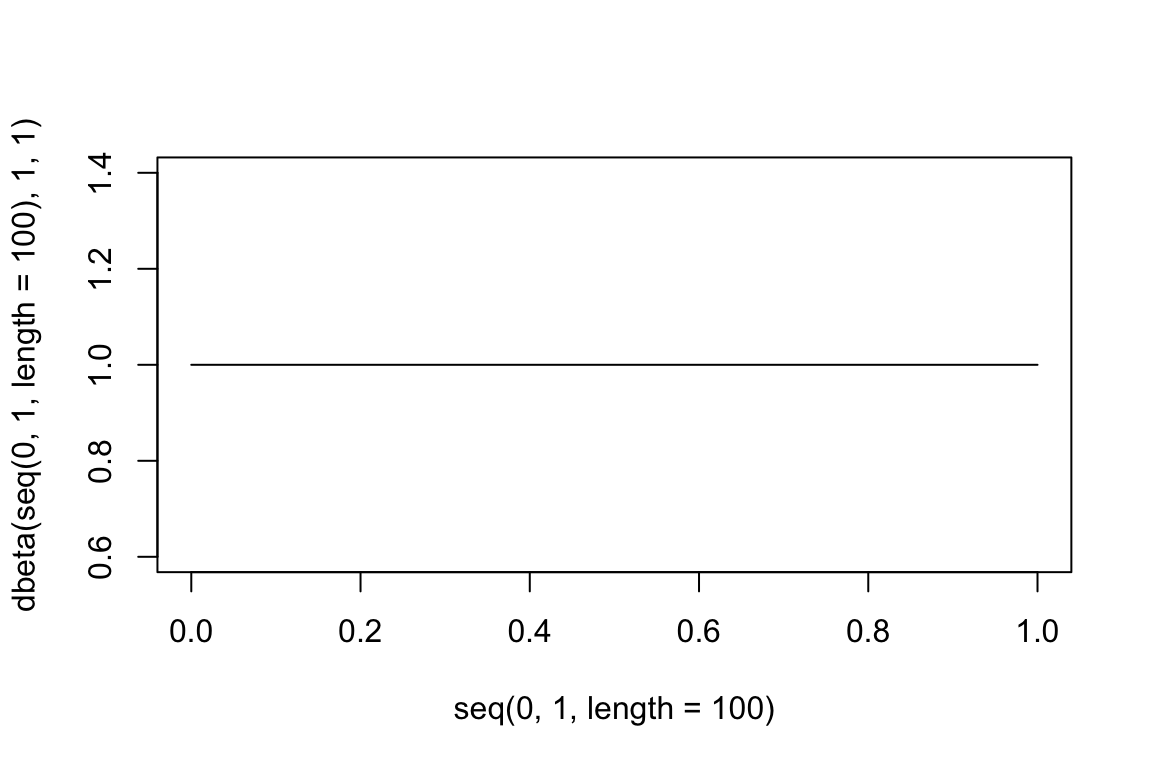
library(slider)

I know enough to know that the distribution that’s being updated is the beta. (Apparently is the binomial. Still a but lost on their distinction!) So I’ll get the density for each update.

plot(
  seq(0,1, length =100),
  dbeta(seq(0,1, length =100), 1, 1),
  type = 'l'
)

water_land_sequence <- c("W", "L", "W", "W", "L", "W", "L", "W")

I’ll use slider::slide() to generate a data frame of sample updates. I’ll need a function that takes a sequence of W and L and converts them into counts.

w_l_count <- function(x){
  tibble(
    water = sum(x == "W"),
    land = sum(x == "L")
  )
}
slide(water_land_sequence, 
      .f = w_l_count, 
      .before = Inf,
      .after = 0) |> 
  bind_rows() |> 
  mutate(seq = row_number()) |> 
  bind_rows(
    tibble(
      water = 0,
      land = 0, 
      seq = 0
    )
  ) |> 
  arrange(seq) ->
  sequence_counts
sequence_counts |> 
  gt()
water land seq
0 0 0
1 0 1
1 1 2
2 1 3
3 1 4
3 2 5
4 2 6
4 3 7
5 3 8
Table 5:

Table of water, land count updates

Now to get the densities.

sequence_counts |> 
  rowwise() |> 
  mutate(
    density = map2(
      water, land, ~tibble(
        prop = seq(0.0001, 0.9999, length = 100),
        density_unstd = dbinom(water, size = water + land, prob = prop),
        density = density_unstd/sum(density_unstd)
        )
    )
  ) |> 
  unnest(density)->
  density_updates
density_updates |> 
  ggplot(aes(prop, density))+
    geom_line(aes(group = seq, color = seq))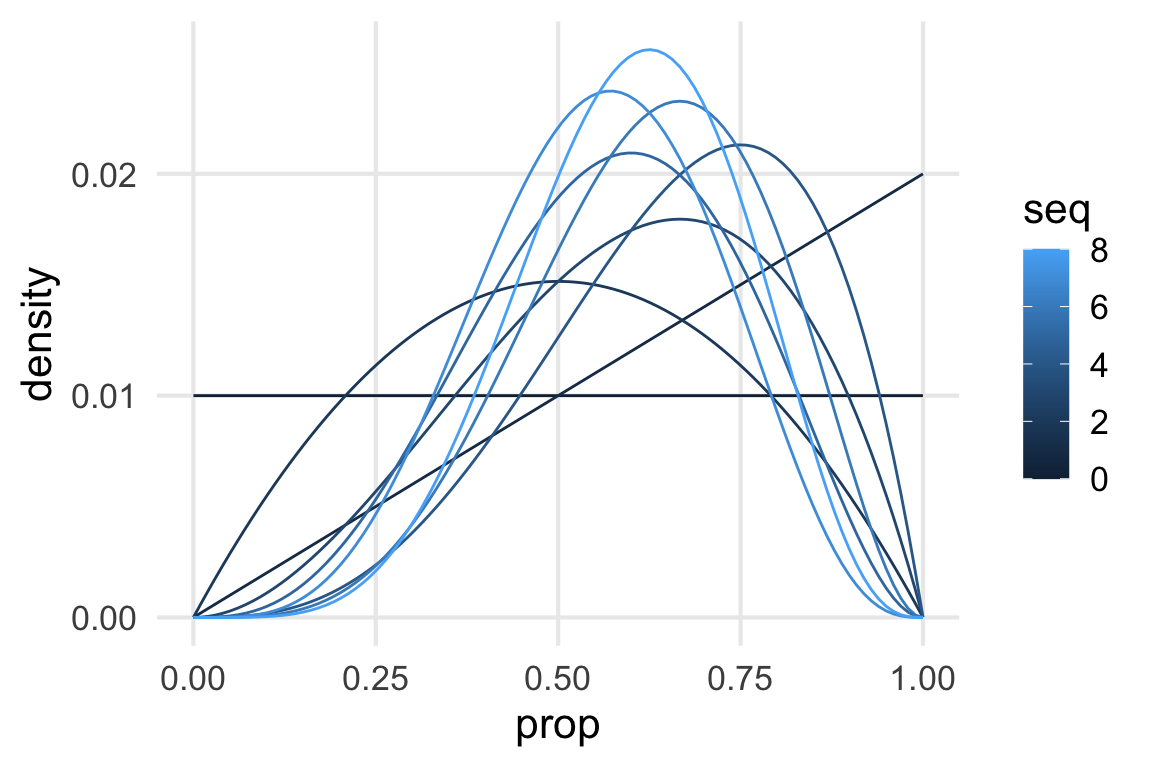

Figure 1: beta distribution updates

Good first step.

I had to turn to the plotly book to get the animated lines correct https://plotly-r.com/animating-views.html.

sequence_counts |> 
  mutate(
    annotation = str_glue("W:{water}, L:{land}")
  ) -> 
  wl_annotate
density_updates |> 
  plot_ly() |> 
  add_lines(
    x = ~prop,
    y = ~density,
    frame = ~seq,
    line = list(simplify = F, width = 3)
  ) |> 
  add_text(
    data = wl_annotate,
    text = ~annotation,
    frame = ~seq,
    x = 0.1,
    y = 0.025,
    textfont = list(size = 20)
  ) |>
  layout(
    showlegend = F
  )

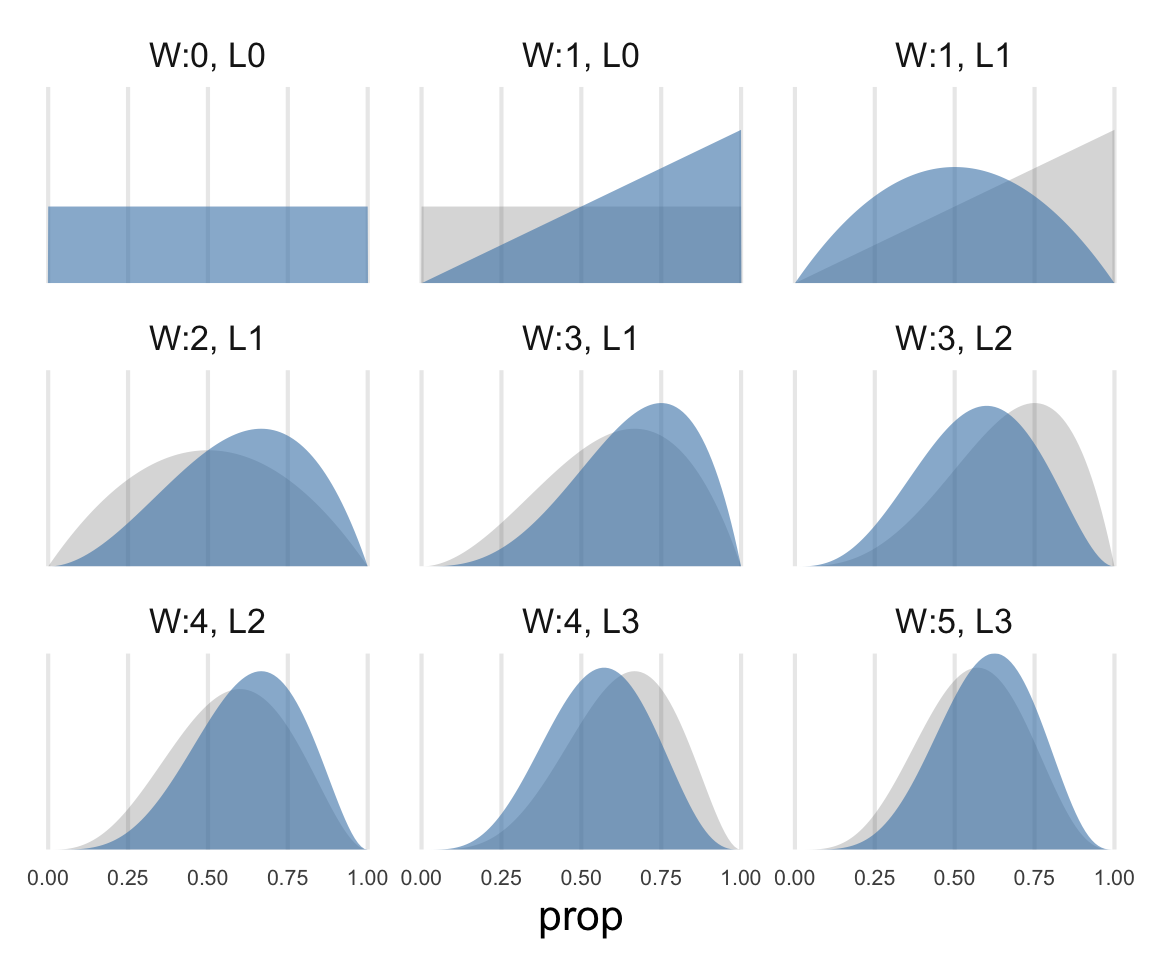
Figure 2: Animated Bayesian Updating

Update: I started making this just for the pdf, which can’t have the animation, but it’s actually kind of nice enough to include in the html.

density_updates |> 
  group_by(prop) |> 
  arrange(seq) |> 
  mutate(
    prev_density = lag(density),
    facet_lab = str_glue("W:{water}, L{land}")
  ) |> 
  ggplot(aes(prop, density))+
    geom_area(aes(y = prev_density), linetype = 2, alpha = 0.2)+
    geom_area(alpha = 0.6, fill = "steelblue")+
    scale_y_continuous(expand = expansion(mult = c(0,0)))+
    facet_wrap(~facet_lab)+
    theme(
      axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      axis.text.x = element_text(size = 8),
      panel.grid.major.y = element_blank()
    )

Figure 3: Static figure of Bayesian Updating

On priors

The fact that statistical inference uses mathematics does not imply that there is only one reasonable or useful way to conduct an analysis.

Grid approximation

Ok, I’ll do one grid approximation for the hell of it.

…

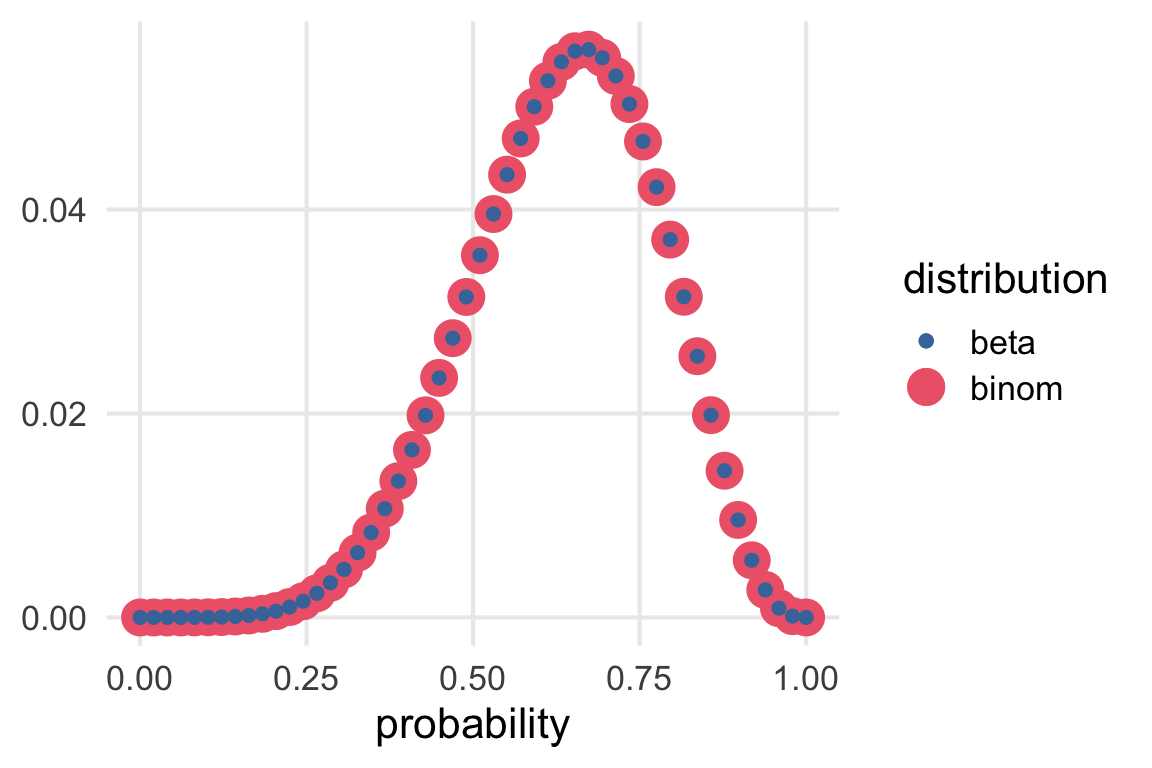
Got distracted and went down a rabbit hole on the beta vs binomial distributions.

tibble(
  prob = seq(0.0001, 0.9999, length = 50), 
  prior_unstd = case_when(
    prob < 0.5 ~ 0,
    .default = 1
  ),
  prior_std = prior_unstd/sum(prior_unstd),
  likelihood_binom = dbinom(6, size = 9, prob = prob),
  l_binom_std = likelihood_binom/sum(likelihood_binom),
  likelihood_beta = dbeta(prob, 6, 9-6),
  l_beta_std = likelihood_beta/sum(likelihood_beta)
) |> 
  ggplot(aes(prob))+
    geom_point(aes(y = l_binom_std, color = "binom"))+
    geom_point(aes(y = l_beta_std, color = "beta"))+
    scale_color_bright()+
    labs(
      x = "probability",
      color = "distribution",
      y = NULL
    )

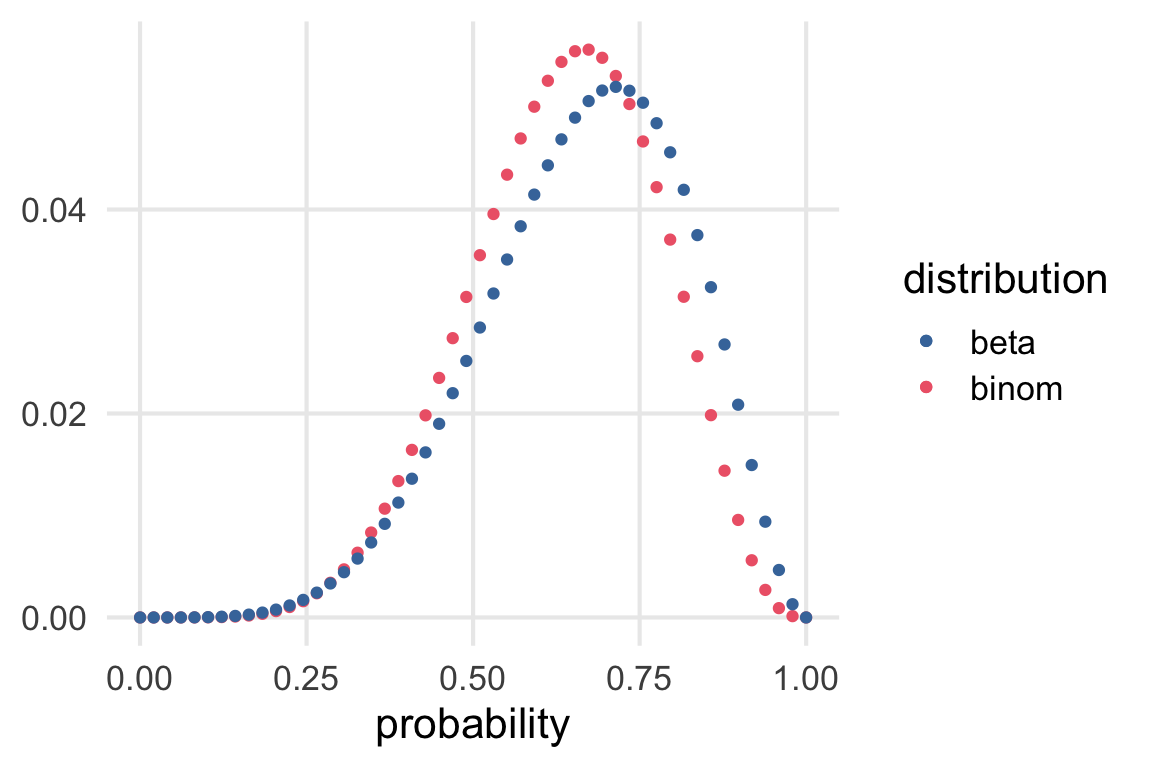
Figure 4: Comparing normalized densities for beta(6,3) and binom(6, 9, p)

Glad I did this. I guess

  • dbinom \(\propto P(O, S | p)\)

  • dbeta \(\propto P(p|O,S)\)

I guess I’d want to see dbinom plotted out with O on the x axis?

tibble(
  probability = seq(0.0001, 0.9999, length = 10)
) |> 
  rowwise() |> 
  mutate(
    densities = map(
      probability,
      ~tibble(obs = 0:9, 
              density = dbinom(obs, size = 9, prob = .x))
    )
  ) |> 
  unnest(densities) ->
  binomial_densities 

binomial_densities |> 
  ggplot(aes(obs, density, color = probability))+
    geom_point()+
    geom_line(aes(group = probability)) +
    geom_rect(
      color = "red",
      fill = NA,
      xmin = 5.5,
      xmax = 6.5,
      ymin = 0,
      ymax = 1
    )+
    scale_color_batlow()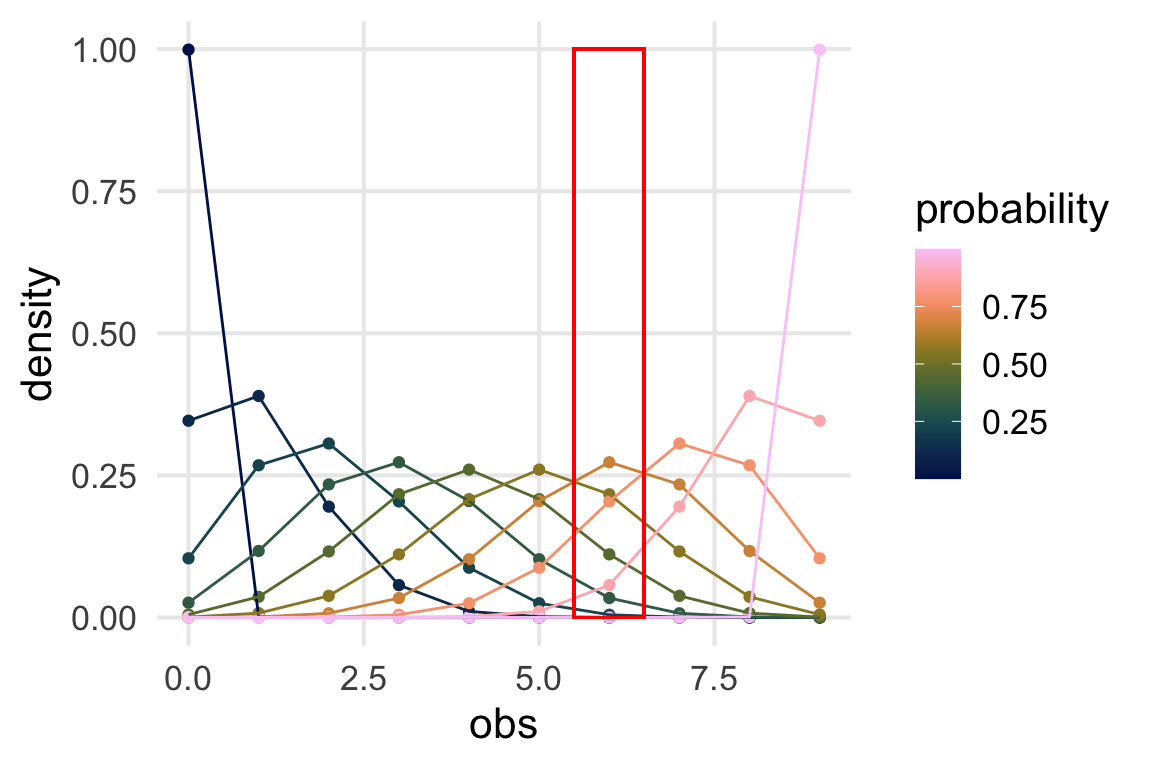

Figure 5: Binomial distributions of various successes out of 9 trials, for various p

What we’re plotting out is what’s in the red box, flipped on its side.

binomial_densities |> 
  filter(obs == 6) |> 
  ggplot(aes(probability, density))+
    geom_line()+
    geom_point(aes(color = probability))+
    scale_color_batlow()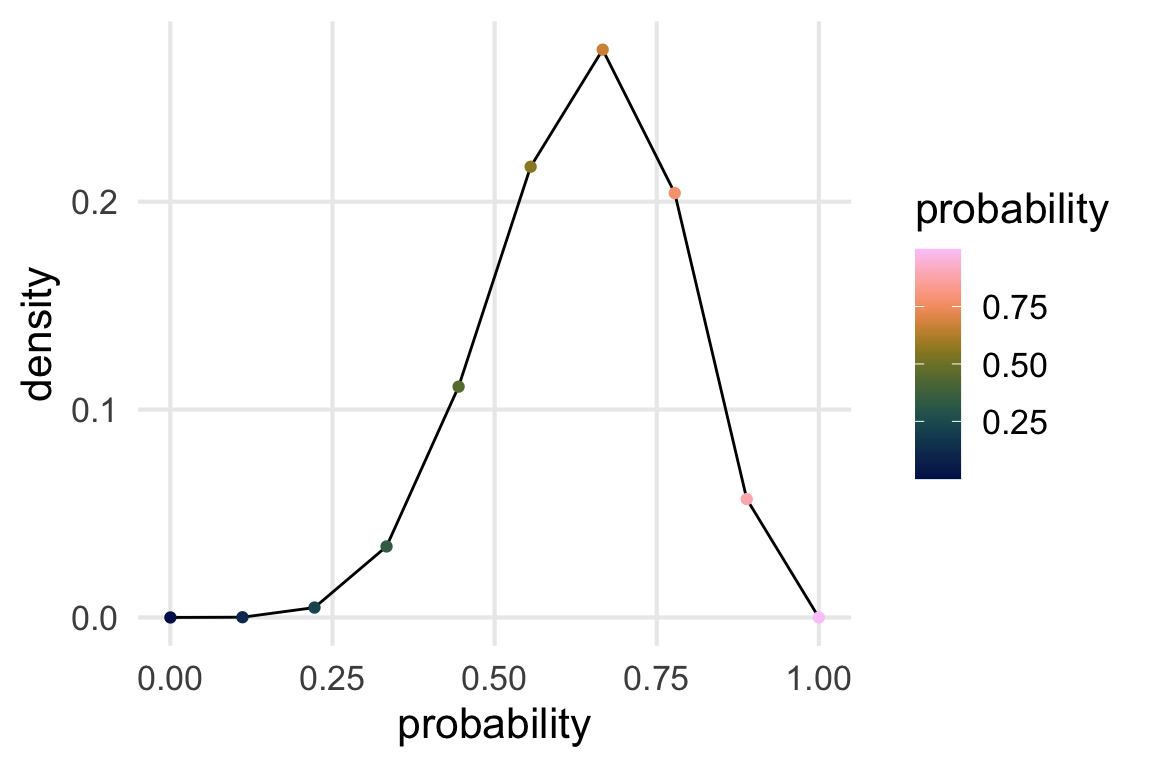

Figure 6: Normalized binomial density for 6 successes out of 9 trials for various p.

Update!

Thanks TJ!

tibble(
  prob = seq(0.0001, 0.9999, length = 50), 
  prior_unstd = case_when(
    prob < 0.5 ~ 0,
    .default = 1
  ),
  prior_std = prior_unstd/sum(prior_unstd),
  likelihood_binom = dbinom(6, size = 9, prob = prob),
  l_binom_std = likelihood_binom/sum(likelihood_binom),
  likelihood_beta = dbeta(prob, (6+1), (9-6)+1),
  l_beta_std = likelihood_beta/sum(likelihood_beta)
) |> 
  ggplot(aes(prob))+
    geom_point(aes(y = l_binom_std, color = "binom", size = "binom"))+
    geom_point(aes(y = l_beta_std, color = "beta",size = "beta"))+
    scale_color_bright()+
    labs(
      x = "probability",
      color = "distribution",
      size = "distribution",
      y = NULL
    )

Figure 7: Comparing normalized densities for beta(6+1,3+1) and binom(6, 9, p)