Predictive Distributions

Listening

One last post to work through different predictive distributions given 6W and 3W.

• The prior predictive distribution.

• The maximum likelihood.

• the posterior predictive distribution.

Loading

library(tidyverse)
library(ggdist)
library(here)
library(ggblend)

source(here("_defaults.R"))

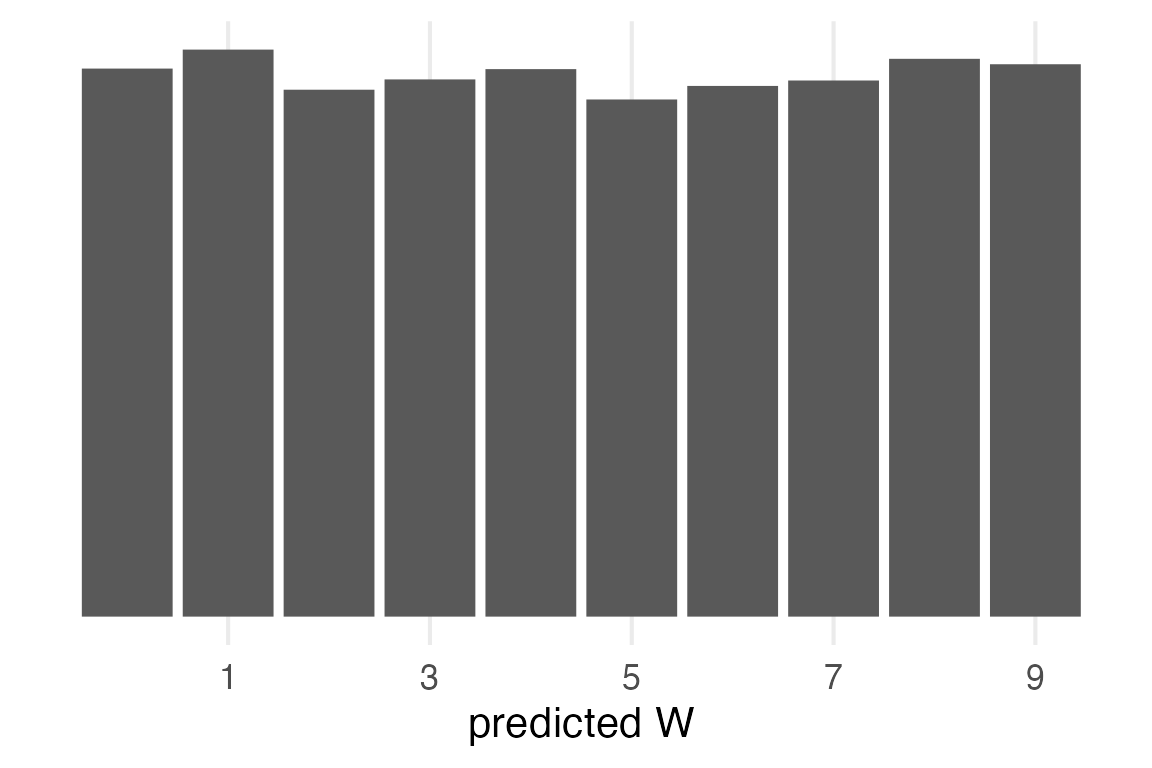
Prior predictive

The prior was a Uniform distribution between 0 and 1, or \(\mathcal{U}(0,1)\). The outcome will also be uniform, but I’ll go through all the steps for completeness.

tibble(
  p = runif(1e4)
) ->
  prior_samp

I’ll make use of vectorization of rbinom() to generate possible samples with probabilities in prior_samp$p.

set.seed(2023)
prior_samp |> 
  mutate(
    pred_binom = rbinom(
      n(), 
      size = 9, 
      prob = p
    )
  ) |> 
  count(pred_binom) |>
  mutate(prob = n/sum(n)) ->
  prior_pred

1

I’m going straight from generated samples to summarising for the distribution.

prior_pred |> 
  ggplot(aes(pred_binom, prob))+
    geom_col()+
    scale_x_continuous(
      name = "predicted W",
      breaks = seq(1, 9, by = 2)
    )+
    theme_no_y()

1

I’ve moved theme_no_y() into _defaults.R which I source at the top.

Maximum Likelihood

The maximum likelihood probability of W is \(\frac{6}{9}=0.6\overline{6}\). We can get predicted values for that probability from binomial distribution.

tibble(
  pred_binom = 0:9,
  dens = dbinom(
    pred_binom, 
    size = 9, 
    prob = 6/9
  ),
  prob = dens
) -> 
  ml_pred

ml_pred |> 
  ggplot(aes(pred_binom, prob))+
    geom_col()+
    scale_x_continuous(
      name = "predicted W",
      breaks = seq(1, 9, by = 2)
    )+
    theme_no_y()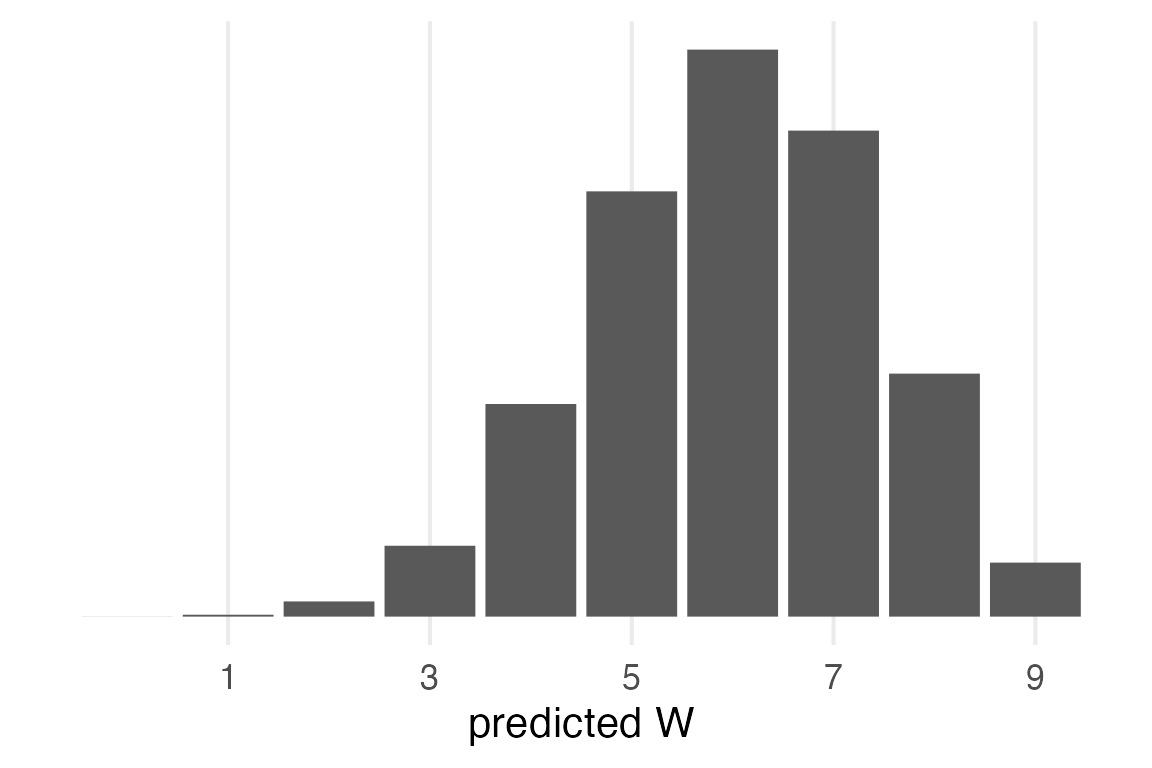

Posterior Prediction

For the posterior prediction, first we sample probabilities from the beta distribution

\[ p \sim \text{Beta}(W+1, L+1) \]

(a.k.a. dbeta())

Then for each \(p\), we generate predictions from the binomial distribution.

\[ Y|p \sim \text{Bin}(9,p) \]

This chapter has been doing grid sampling, but I’ll just use the rbeta() function for simplicity.

tibble(
  p = rbeta(1e4, 6+1, 3+1)
) ->
  posterior_samp

Then, it’s the same operation as the prior predictive distribution.

posterior_samp |> 
   mutate(
    pred_binom = rbinom(
      n(), 
      size = 9, 
      prob = p
    )
  ) |> 
  count(pred_binom) |> 
  mutate(prob = n/sum(n)) ->
  posterior_pred

posterior_pred |> 
  ggplot(aes(pred_binom, prob))+
    geom_col() +
    scale_x_continuous(
      name = "predicted W",
      breaks = seq(1, 9, by = 2)
    ) +
    theme_no_y()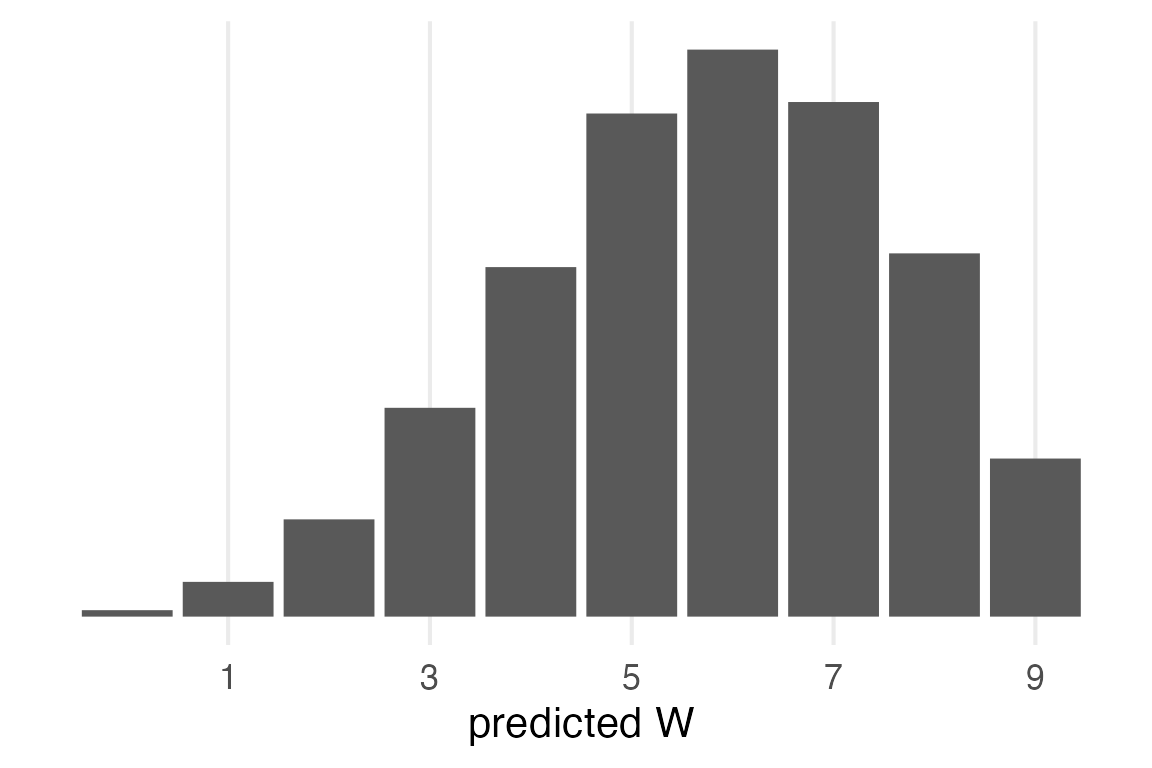

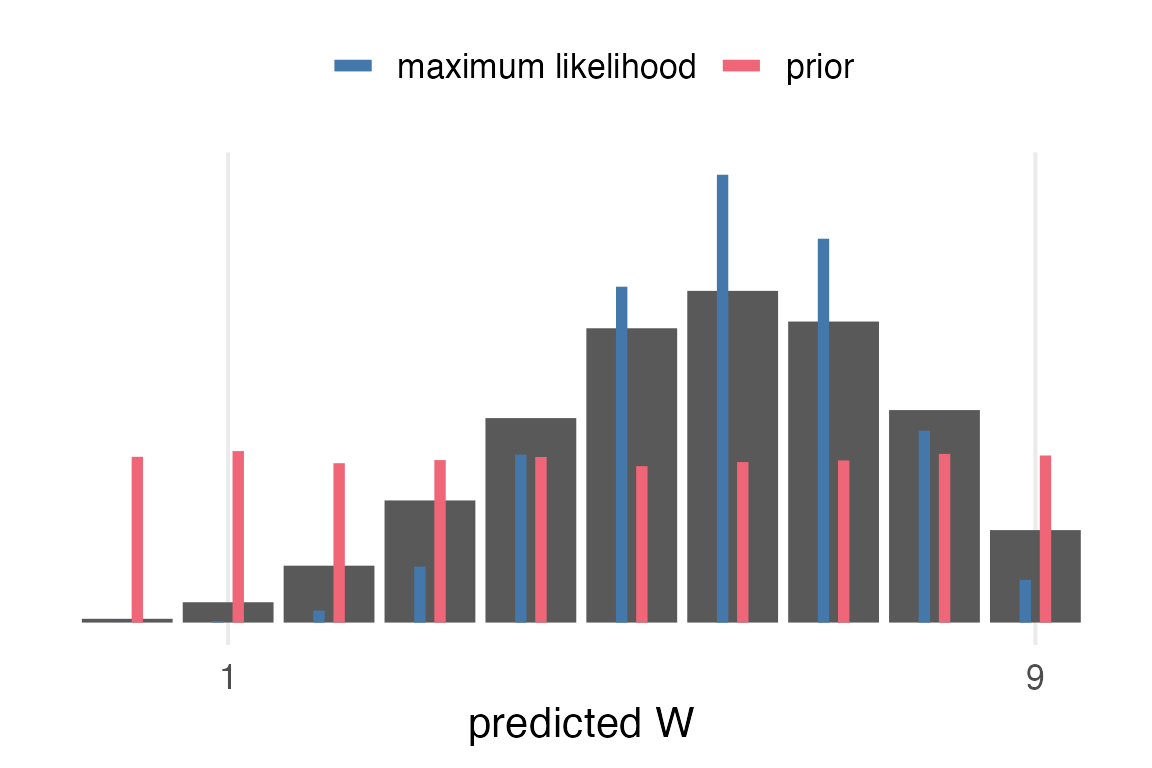
Comparisons

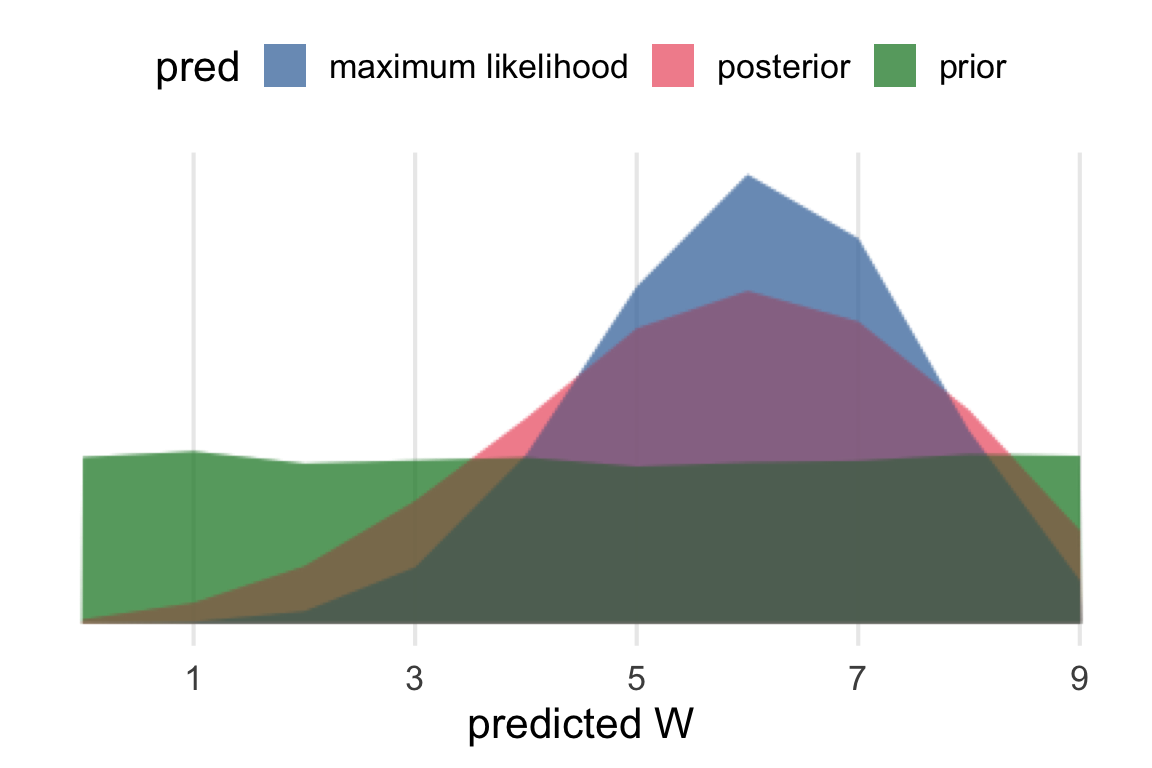
Now, I want to compare the posterior predictive distribution to the maximum likelihood and the prior. This is one concept I had, which has the prior and the ML values as thinner bars within the posterior predictive bars.

posterior_pred |> 
  ggplot(aes(pred_binom, prob))+
    geom_col()+
    geom_segment(
      data = ml_pred,
      aes(
        x = pred_binom-0.1,
        xend = pred_binom-0.1,
        yend = 0,
        color = "maximum likelihood"
      ),
      linewidth = 2
    )+
    geom_segment(
      data = prior_pred,
      aes(
        x = pred_binom+0.1,
        xend = pred_binom+0.1,
        yend = 0,
        color = "prior"
      ),
      linewidth = 2
    )+  
    scale_x_continuous(
      breaks = seq(1, 9, length = 2)
    )+
    labs(
      color = NULL,
      x = "predicted W"
    )+
    theme_no_y()+
    theme(
      legend.position = "top"
    )

Overplotting them is also a possibility, and a good occasion to test out {ggblend}. I had some issues getting this to work with the available graphic devices & quarto.

```{r}
#| dev: "png"
#| dev-args:
#|   - type: "cairo"
bind_rows(
  posterior_pred |> 
    mutate(pred = "posterior"),
  ml_pred |> 
    mutate(pred = "maximum likelihood"),
  prior_pred |> 
    mutate(pred = "prior")
) |> 
  ggplot(aes(pred_binom, prob, fill = pred))+
    geom_area(position = "identity", alpha = 0.5) * 
      (blend("lighten") + blend("darken")) +
    scale_x_continuous(
      name = "predicted W",
      breaks = seq(1, 9, by = 2)
    )+
    theme_no_y()+
    theme(
      legend.position = "top"
    )
```

Visualizing the posterior prediction process

posterior_samp |> 
  slice(1:4) |> 
  mutate(
    pred_binom = rbinom(
      n(), 
      size = 9, 
      prob = p
    )
  ) |> 
  arrange(
    p
  ) ->
  example_samp

example_samp |> 
  mutate(
    dens = dbeta(p, 6+1, 3+1),
    n = row_number()
  )->
  example_samp

tibble(
  p = seq(0, 1, length = 100),
  dens = dbeta(p, 6+1, 3+1)
) |> 
  ggplot(aes(p, dens))+
    geom_area(fill = "grey") +
    geom_segment(
      data = example_samp,
      aes(
        xend = p,
        yend = 0,
        color = factor(n)
      ),
      linewidth = 1.5,
      lineend = "round",
      show.legend = F
    )+
    theme_no_y()+
    labs(
      title = "Posterior"
    )->
  posterior_plot

This involved messing around with {rlang} data masking that I still don’t quite follow. Both the p and pred arguments had to be (just once!) prefixed with !!, but not n.

sample_plot_fun <- function(p, pred, n){
  this_scale <- as.vector(khroma::color("bright")(4))
  tibble(
    ws = 0:9,
    dens = dbinom(ws, size = 9, prob = !!p)
  ) |> 
    ggplot(aes(ws, dens))+
      geom_col(
        aes(fill = ws == !!pred)
      )+
      scale_fill_manual(
        values = c("grey", this_scale[n]),
        guide = "none"
      ) +
      scale_x_continuous(
        breaks = seq(1,9, by = 2)
      )+
      labs(
        x = "prediction",
        title = str_glue("p = {round(p, digits = 2)}")
      ) +
      theme_no_y()+
      theme(
        plot.title = element_text(size = 10)
      )
}

example_samp |> 
  rowwise() |> 
  mutate(
    plot = list(
      sample_plot_fun(p, pred_binom, n)
    )
  )->
  samp_plots

library(patchwork)

Going to use some patchwork and purr::reduce() fanciness.

posterior_plot/
(samp_plots |> 
  ungroup() |> 
  pull(plot) |> 
  reduce(.f = `+`) +
  plot_layout(nrow = 1))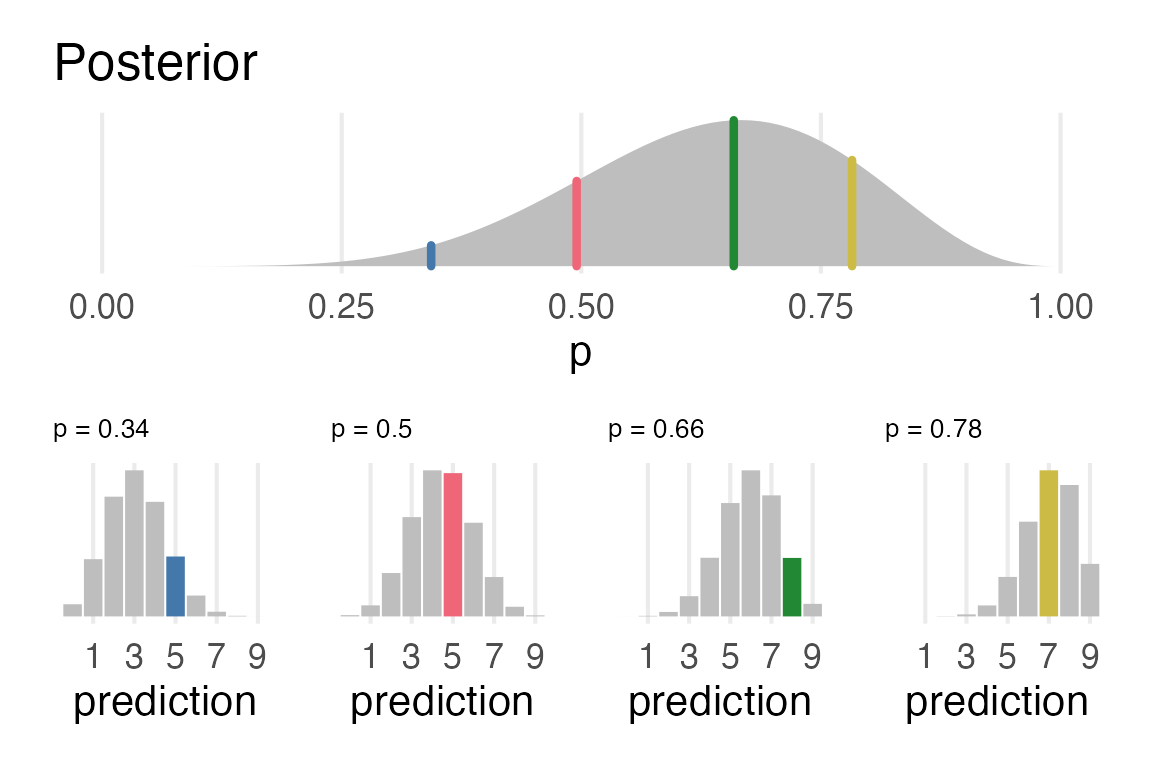

Pretty pleased with this!