Reporting a linear model

Author

Josef Fruehwald

Published

June 14, 2023

Listening

Loading

library(tidyverse)
library(tidybayes)
library(gt)

library(brms)
library(marginaleffects)
library(broom.mixed)

source(here::here("_defaults.R"))

The plan

Part of why I’m working through Statistical Rethinking as a blog is so that I can take some time and mess around with finessing how I’ll visualize and report models like this, so I’m going to try to work over these basic models I just fit.

Data loading, prep, and model fits

read_delim(
  "https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Howell1.csv", 
  delim = ";"
) ->
  Howell1
stable_height <- Howell1 |> 
  filter(age >= 30)

stable_height |> 
  mutate(
    weight0 = weight-mean(weight)
  )->
  height_to_mod
height_formula <- bf(
  height ~ 1
)
c(
  prior(
    prior = normal(178, 20),
    class = Intercept
  ),
  prior(
    prior = uniform(0,50),
    lb = 0,
    ub = 50,
    class = sigma
  )
) ->
  height_mod_priors
brm(
  height_formula,
  prior = height_mod_priors,
  family = gaussian,
  data = stable_height,
  sample_prior = T,
  save_pars = save_pars(all = TRUE),
  file = "height_mod.rds",
  file_refit = "on_change"
) ->
  height_mod
height_weight_formula <- bf(
  height ~ 1 + weight0
)
height_weight_priors <- c(
  prior(
    prior = normal(178, 20),
    class = Intercept
  ),
  prior(
    prior = uniform(0,50),
    lb = 0,
    ub = 50,
    class = sigma
  ),
  prior(
    prior = normal(0,10),
    class = b
  )
)
brm(
  height_weight_formula,
  prior = height_weight_priors,
  data = height_to_mod, 
  file = "height_weight_mod.rds",
  save_pars = save_pars(all = TRUE),
  file_refit = "on_change"
) ->
  height_weight_mod

First look - Model Fit

Posterior predictive check

First I’ll go with the default type of pp_check()

pp_check(height_mod, ndraws = 100)+
  khroma::scale_color_bright()+
  labs(
    color = NULL,
    title = "height ~ 1"
  )+
  theme_no_y()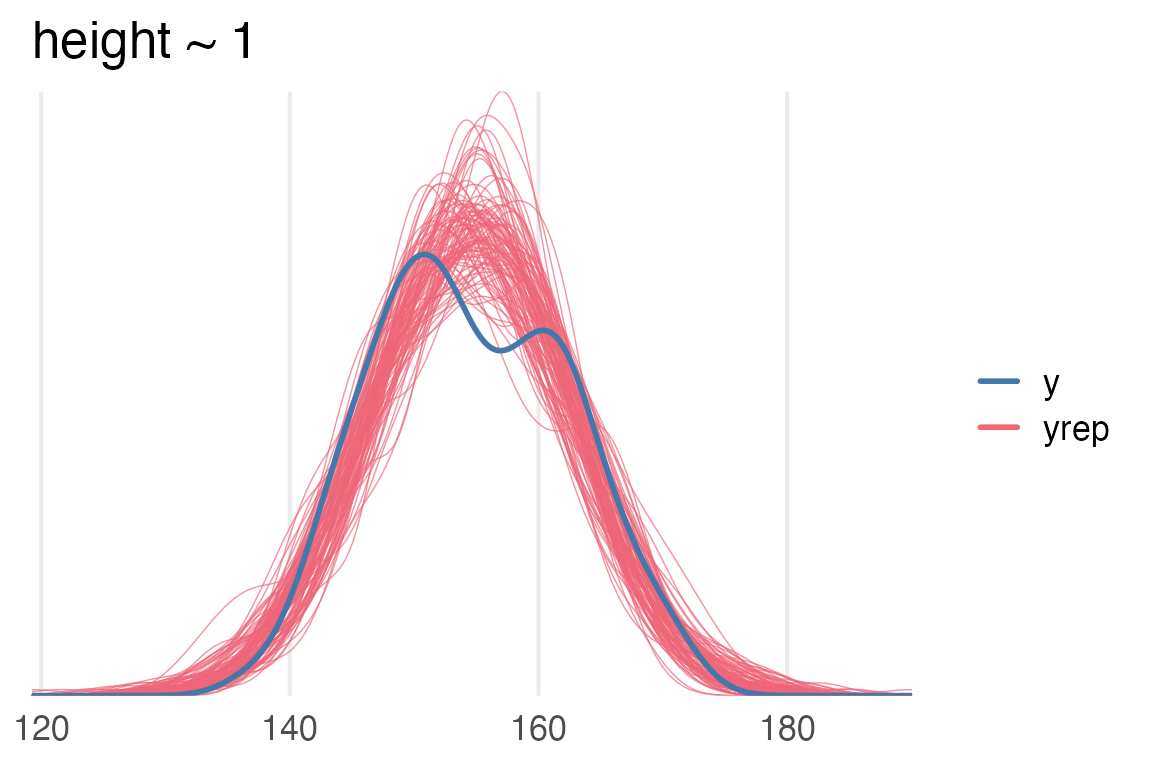

Figure 1: Posterior preditctive check for the height~1 model

So, the distribution of posterior predictions for the intercept only model puts a lot of probability where there’s an actual dip in the original data.

pp_check(height_weight_mod, ndraws = 100)+
  khroma::scale_color_bright()+
  labs(
    color = NULL,
    title = "height ~ weight"
  )+
  theme_no_y()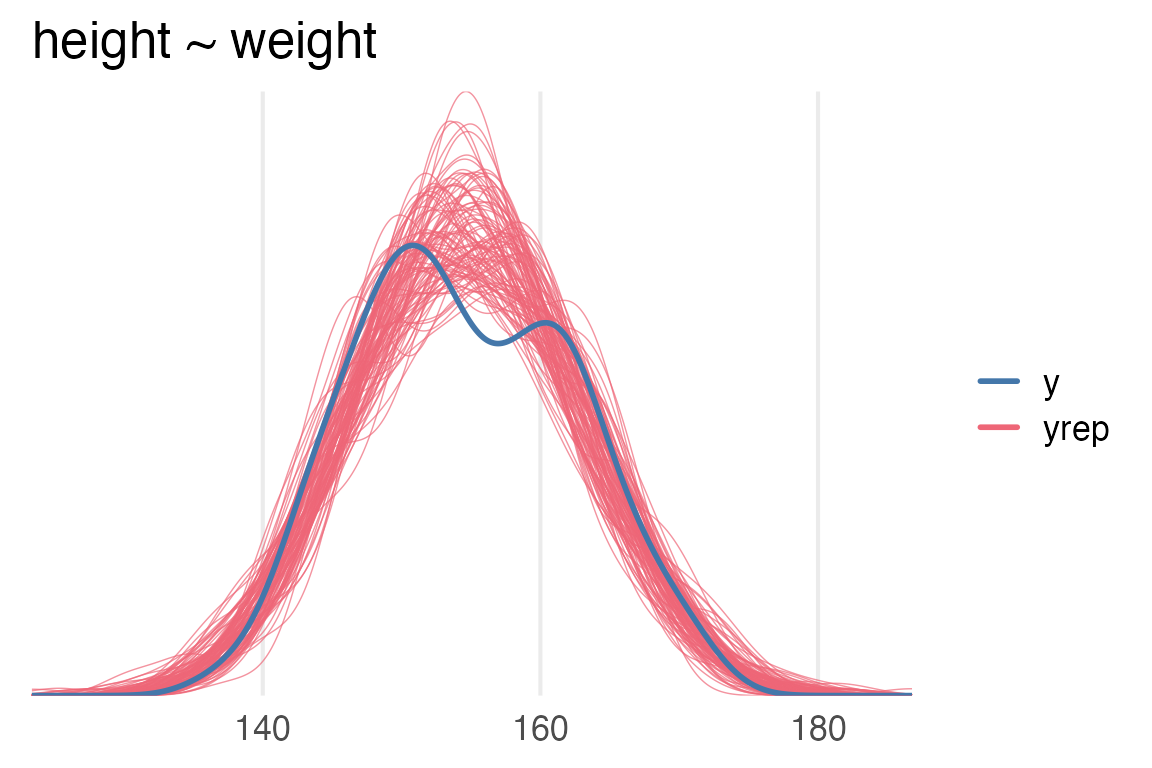

Figure 2: Posterior predictive check for the height ~ weight model.

\(R^2\)

Let’s get some goodness of fit parameters. {brms} / {rstantools} have bayes_R2() which cites Gelman et al. (2019). Classic \(R^2\) is \(1-\frac{\text{residuals variance}}{\text{data variance}}\). As Gelman et al. (2019) point out, there’s no one set of residuals, since the model parameters are all distributions rather than point estimates, so they propose an \(R^2\) for Bayesian models as \(\frac{\text{variance of fitted values}}{\text{variance of fitted values} + \text{variance of residuals}}\), for sampled fitted values and their respective residuals.

But, as they say

A new issue then arises, though, when fitting a set of a models to a single dataset. Now that the denominator of \(R^2\) is no longer fixed, we can no longer interpret an increase in \(R^2\) as a improved fit to a fixed target.

I’m glad I read the paper!

Anyways, height_mod has an \(R^2\) of 0, as it should as an intercept only model.

bayes_R2(height_mod)
   Estimate Est.Error Q2.5 Q97.5
R2        0         0    0     0

I had to think for a second about how this made sense, but as an intercept only model, the predicted values for the data will be just a single number, equal to the intercept \(\mu\).

predictions(
  height_mod 
) |> 
  posterior_draws() ->
  height_fitted

height_fitted |> 
  filter(drawid == "1") |> 
  slice(1:6) |> 
  rmarkdown::paged_table()

I computed \(R^2\) by hand here. I’m a bit lost why the variance of the residuals is identical for every draw…

height_fitted |> 
  mutate(resid = height - draw) |> 
  group_by(drawid) |> 
  summarise(
    var_fit = var(draw),
    var_resid = var(resid)
  ) |> 
  mutate(bayesr2 = var_fit/(var_fit+var_resid)) |> 
  slice(1:6) |> 
  rmarkdown::paged_table()

The \(R^2\) for the height~weight model is about 0.57

bayes_R2(height_weight_mod)
   Estimate  Est.Error      Q2.5    Q97.5
R2 0.572246 0.02644878 0.5143232 0.618783

Let’s try calculating that “by hand” again.

predictions(
  height_weight_mod
) |> 
  posterior_draws() |> 
  mutate(resid = height - draw) |> 
  group_by(drawid) |> 
  summarise(
    var_fit = var(draw),
    var_resid = var(resid)
  ) |> 
  mutate(bayesr2 = var_fit / (var_fit + var_resid)) |> 
  mean_qi(bayesr2)
# A tibble: 1 × 6
  bayesr2 .lower .upper .width .point .interval
    <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
1   0.572  0.514  0.619   0.95 mean   qi

Cool. We can get this all from bayes_R2() also.

bayes_R2(height_weight_mod, summary = F) |> 
  as_tibble() |> 
  ggplot(aes(R2))+
    stat_slab()+
    scale_y_continuous(
      expand = expansion(mult = 0)
    )+
    xlim(0,1)+
    labs(
      x = expression(R^2)
    )+
    theme_no_y()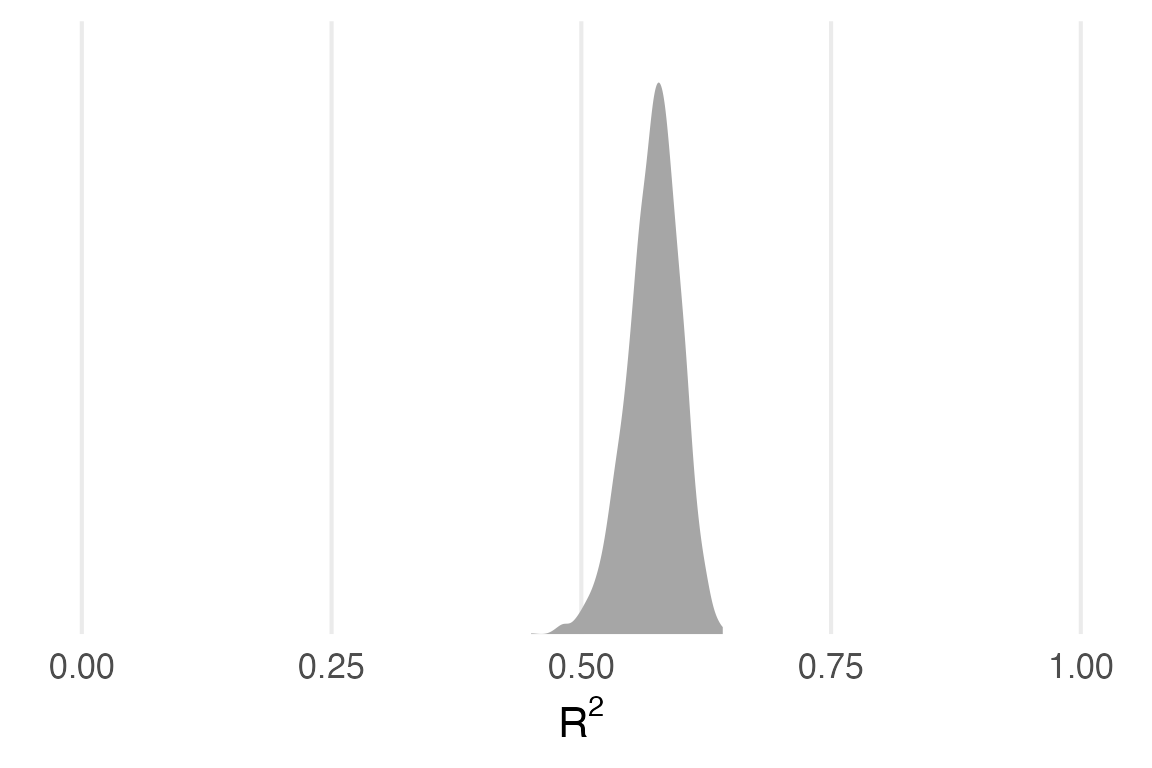

Figure 3: Estimate of Bayesian \(R^2\)

loo

Ok… Time to understand what loo() does, and what elpd means. Doing my best with Vehtari, Gelman, and Gabry (2016)

elpd

Expected Log Pointwise Predictive Density (we lost a “p” somewhere).

Starting with lpd (log pointwise predictive density). So \(p(y_i|y)\) is the probability of a data point \(y_i\) given the distribution of data \(y\). We log it, probably to keep things computable and addition based, and sum it up across every datapoint, \(\sum \log p(y_i|y)\). This is apparently equal to \(\sum \log \int p(y_i|\theta)p(\theta|y)d\theta\).

  • \(p(y_i|\theta)\) = the probability of each data point given the model

  • \(p(\theta|y)\) = the probability of the model given the data.

Ok, but \(p(y_i | y)\) is derived from probabilities over models that had seen \(y_i\). \(p(y_i|y_{-i})\) is the probability of data point \(y_i\) derived from a model that had not seen \(y_i\), a.k.a. “leave one out”. ELPD is the summed up log probabilities across these leave-one-out models.

As best as I can tell, the rest of the paper is just about getting very clever about how to approximate \(\sum \log p(y_i|y_{-i})\) without needing to refit the model for each datapoint. It’s this cleverness that will sometimes result in a warning about “Pareto k estimates”

So, without any further ado:

loo(height_mod)

Computed from 4000 by 251 log-likelihood matrix

         Estimate   SE
elpd_loo   -874.6  8.9
p_loo         1.7  0.2
looic      1749.2 17.8
------
Monte Carlo SE of elpd_loo is 0.0.

All Pareto k estimates are good (k < 0.5).
See help('pareto-k-diagnostic') for details.

So, if the leave-one-out probability of each data point was higher, the elpd_loo value would be closer to 0, aka exp(0)= 1.

loo(height_weight_mod)

Computed from 4000 by 251 log-likelihood matrix

         Estimate   SE
elpd_loo   -768.9 12.9
p_loo         3.2  0.6
looic      1537.7 25.8
------
Monte Carlo SE of elpd_loo is 0.0.

All Pareto k estimates are good (k < 0.5).
See help('pareto-k-diagnostic') for details.

To compare the two models:

loo_compare(
  loo(height_mod),
  loo(height_weight_mod)
)
                  elpd_diff se_diff
height_weight_mod    0.0       0.0 
height_mod        -105.8      12.7

So, the height-only model has a worse elpd. And we can be pretty sure it’s a worse elpd, because dividing it by the standard error of the difference is about -8, which according to the Stan discussion forums is a pretty big difference.

Wrapping it into a report

Posterior predictive checks of both models show considerable bimodality is not sufficiently captured by either the intercept-only model or the weight model.

Code 
posterior_predict(height_mod) |> 
  as.data.frame() |> 
  mutate(.draw = row_number()) |> 
  slice(1:100) |> 
  pivot_longer(-.draw) |> 
  mutate(model = "height ~ 1")->
  height_pp

posterior_predict(height_weight_mod) |> 
  as.data.frame() |> 
  mutate(.draw = row_number()) |> 
  slice(1:100) |> 
  pivot_longer(-.draw) |> 
  mutate(model = "height ~ weight")->
  height_weight_pp
  
height_to_mod |> 
  mutate(model = NULL)->
  orig

bind_rows(height_pp, height_weight_pp) |> 
  ggplot(aes(value))+
    stat_density(
      aes(color = "yrep", group = .draw),
      fill = NA,
      position = "identity",
      geom = "line",
      alpha = 0.1
    )+
    stat_density(
      data = orig,
      aes(x = height, color = "y"),
      fill = NA,
      geom = "line",
      linewidth = 1
    )+
    scale_y_continuous(expand = expansion(mult = 0))+
    labs(
      color = NULL
    )+
    facet_wrap(~model)+
    theme_no_y()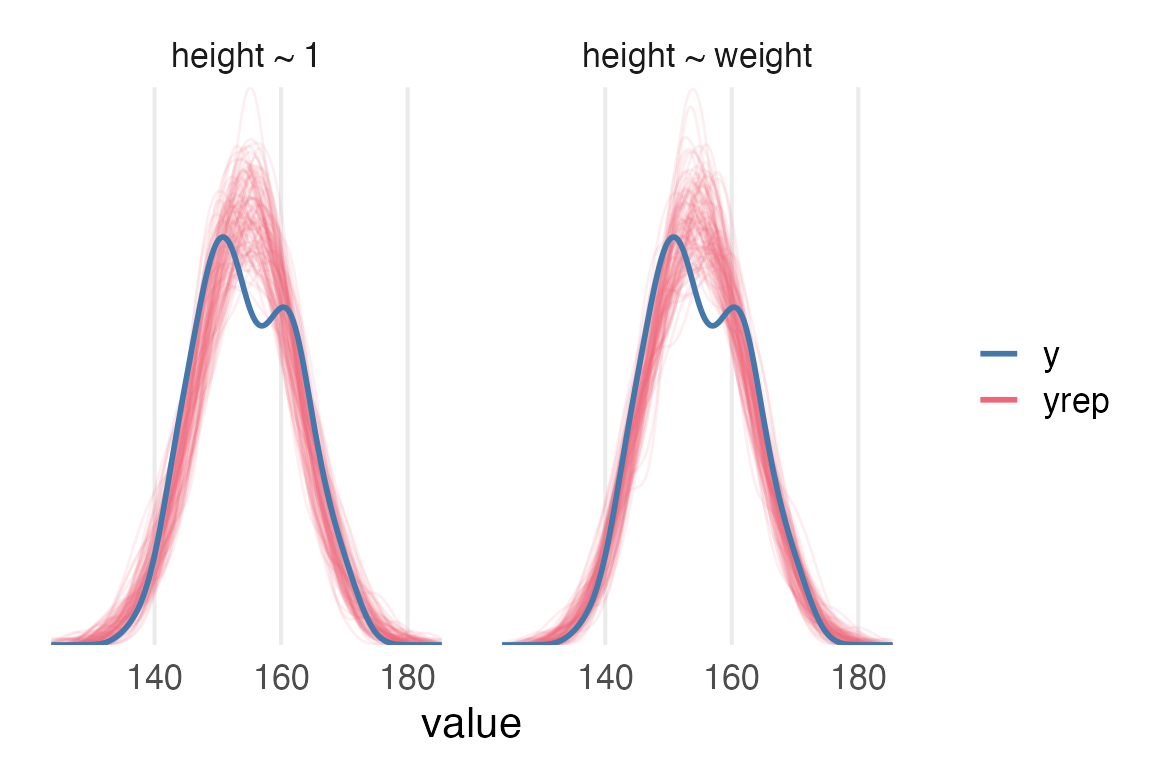

Figure 4: Posterior predictive checks for the two models

Code 
bayes_R2(height_weight_mod, summary = F) |> 
  as_tibble() |> 
  mean_hdci(.width = 0.95) ->
  mod_r2

The intercept-only model necessarily has an \(R^2\) of 0. Mean Bayesian \(R^2\) for the weight model is 0.57 (95% highest density interval of [0.52, 0.62]).

Table 1 displays model comparisons using Leave-One-Out Expected Log Pointwise Predictive Distribution (ELPD) (Vehtari, Gelman, and Gabry 2016).

Code 
loo_compare(
  loo(height_mod),
  loo(height_weight_mod)
) |> 
  as.data.frame() |> 
  rownames_to_column() |> 
  mutate(
    model = case_when(
      rowname == "height_mod" ~ "height ~ 1",
      rowname == "height_weight_mod" ~ "height ~ weight"
    )
   ) |> 
  select(model, elpd_diff, se_diff) |> 
  mutate(ratio = elpd_diff/se_diff) |> 
  gt() |> 
    fmt_number() |> 
    sub_missing() |> 
    cols_label(
      elpd_diff = "ELPD difference",
      se_diff = "difference SE",
      ratio  = "diff/se"
    )
model ELPD difference difference SE diff/se
height ~ weight 0.00 0.00 —
height ~ 1 −105.75 12.66 −8.35
Table 1:

Leave-One-Out Expected Log Pointwise Predictive Distribution comparsion of the two models. ELPD difference contain the difference from the largest LOO ELPD.

Next time:

Writing up a report on the actual parameters.

References

Gelman, Andrew, Ben Goodrich, Jonah Gabry, and Aki Vehtari. 2019. “R-Squared for Bayesian Regression Models.” The American Statistician 73 (3): 307–9. https://doi.org/10.1080/00031305.2018.1549100.
Vehtari, Aki, Andrew Gelman, and Jonah Gabry. 2016. “Practical Bayesian Model Evaluation Using Leave-One-Out Cross-Validation and WAIC.” Statistics and Computing 27 (5): 1413–32. https://doi.org/10.1007/s11222-016-9696-4.