Statistical Rethinking Workthrough Blog - 02 Small Worlds and Large Worlds

listening

In the analogy, models are “Small”, self-contained worlds.

Within the small world, all possibilities are nominated.

Garden of forking paths.

I was thinking of working out the probabilities by doing random sampling…

library(tidyverse)
library(gt)
library(patchwork)
library(here)
source(here("_defaults.R"))

Generating the marble dataframe

tibble(
  blue_marbs = 0:4,
  white_marbs = 4 - blue_marbs
) |> 
  rowwise() |> 
  mutate(
    marbles = list(c(rep("blue", blue_marbs), rep("white", white_marbs)))
  ) -> 
  marbles

marbles |> 
  gt()

blue_marbs	white_marbs	marbles
0	4	white, white, white, white
1	3	blue, white, white, white
2	2	blue, blue, white, white
3	1	blue, blue, blue, white
4	0	blue, blue, blue, blue

Table 1:

The marble sampling distributions

In retrospect, I’m glad I did this, because I thought we were sampling without replacement.

Here’s a function that will repeatedly sample from a set of marbles, and compare the result to a reference group.

sampling_df <- function(marbles, n = 1000, size = 3, pattern = c("blue", "white", "blue")){
  sampling_tibble <- tibble(samp = 1:n)
  sampling_tibble |> 
    mutate(
      chosen = map(samp, ~sample(marbles, size = 3, replace = T)),
      match = map_lgl(chosen, ~all(.x == pattern))
    ) |> 
    summarise(prop_match = mean(match))->
    sampling_tibble
  return(sampling_tibble)
}

1: I’ll capture everything within a tibble.
2: Rowwise, sample from marbles with replacement.
3: Return T or F if the sequence matches the pattern exactly.
4: The mean() of the T, F column to get the proportion that match.

sampling_df(
  marbles = marbles$marbles[[4]],
  n = 5000
)

# A tibble: 1 × 1
  prop_match
       <dbl>
1      0.140

marbles |> 
 ungroup() |> 
  mutate(
    prob = map(marbles, ~sampling_df(.x, n = 10000))
  ) |> 
  unnest(prob) |> 
  mutate(norm_probs = prop_match/sum(prop_match))->
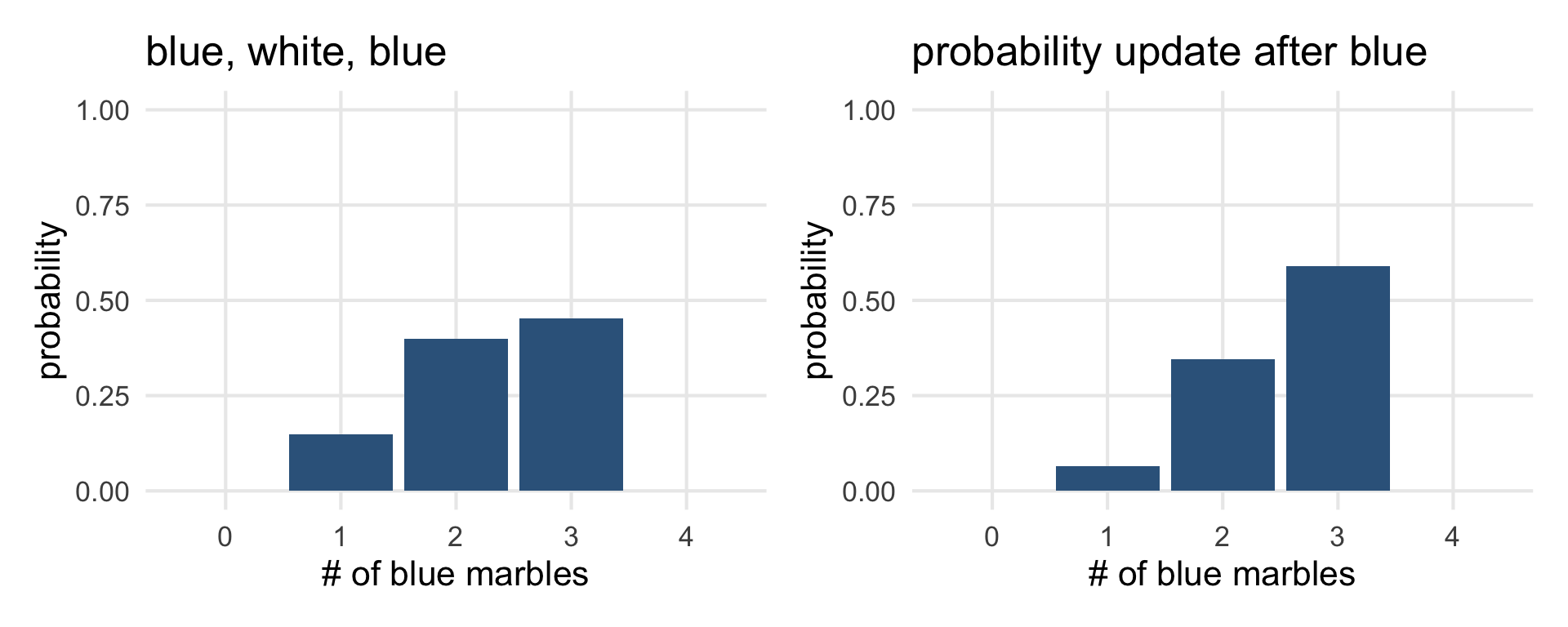
  marble_probs

marble_probs |> 
  ggplot(aes(blue_marbs, norm_probs))+
    geom_col(fill = "steelblue4")+
    labs(
      title = "blue, white, blue",
      x = "# of blue marbles",
      y = "probability"
    ) + 
  ylim(0,1)->probs1
probs1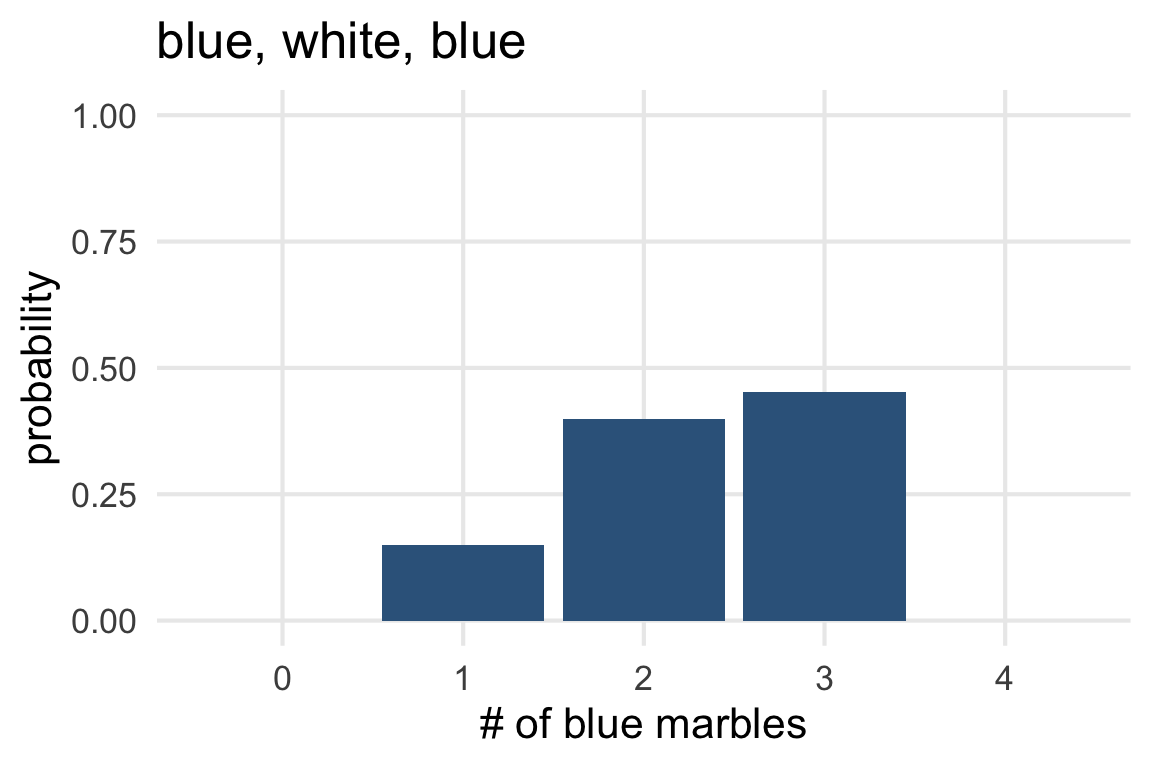

Figure 1: Probability of each composition of marbles

Updating probabilities

What if we draw one more blue

marble_probs |> 
  mutate(new_obs_prob = blue_marbs / sum(blue_marbs),
         posterior_prob = norm_probs * new_obs_prob,
         posterior_norm = posterior_prob/sum(posterior_prob))->
  marble_probs

marble_probs |> 
  ggplot(aes(blue_marbs, posterior_norm))+
    geom_col(fill = "steelblue4")+
    ylim(0,1)+
      labs(
      title = "probability update after blue",
      x = "# of blue marbles",
      y = "probability"
    ) ->
  probs2

probs1 | probs2