Statistical Rethinking Workthrough Blog

Listening

library(tidyverse)
library(broom)
library(patchwork)
library(here)
library(gt)
source(here("_defaults.R"))

Classic Base Rate Issues

flowchart TD
  p["population<br>10,000 individuals"] --> |0.01| v["🧛‍♂️<br>100 individuals"]
  p--> |0.99| h["👨<br>9,900 individuals"]
  
  v --> |0.95| vpos["🧛‍♂️➕<br>95 individuals"]
  v --> |0.05| vneg["🧛‍♂️➖Test Negative<br>5 individuals"]
  
  h --> |0.01| hpos["👨➕<br>99 individuals"]
  h --> |0.99| hneg["👨➖Test Negative<br>9,801 individuals"]
  
  vpos --o pos["(🧛‍♂️,👨)➕<br>194"]
  hpos --o pos
  
  vneg --o neg["(🧛‍♂️, 👨)➖<br>9806"]
  hneg --o neg

Plot of the base rate vs P(vampire | positive test)

tibble(
  # might as well get logarithmic
  base_rate = 10^(seq(-3, -1, length = 20)),
  vamp_and_pos = base_rate * 0.95,
  vamp_and_neg = base_rate * 0.05,
  human_and_pos = (1-base_rate) * 0.01,
  human_and_neg = (1-base_rate) * 0.99,
  p_vamp_pos = vamp_and_pos/(vamp_and_pos + human_and_pos), 
  p_hum_neg = human_and_neg/(vamp_and_neg + human_and_neg)
) -> test_metrics

test_metrics |> 
  ggplot(aes(base_rate, p_vamp_pos))+
    geom_point(color = "steelblue", 
               size = 3)+
    geom_line(color = "steelblue",
              linewidth = 1)+
    scale_x_log10()+
    ylim(0,1)+
    labs(x = "P(vampire)",
         y = "P(vampire | positive)",
         subtitle = "P(positive | vampire) = 0.95\nP(positive | human) = 0.01",
         title = "Positive Predictive Value") +
    theme(plot.subtitle = element_text(size = 12))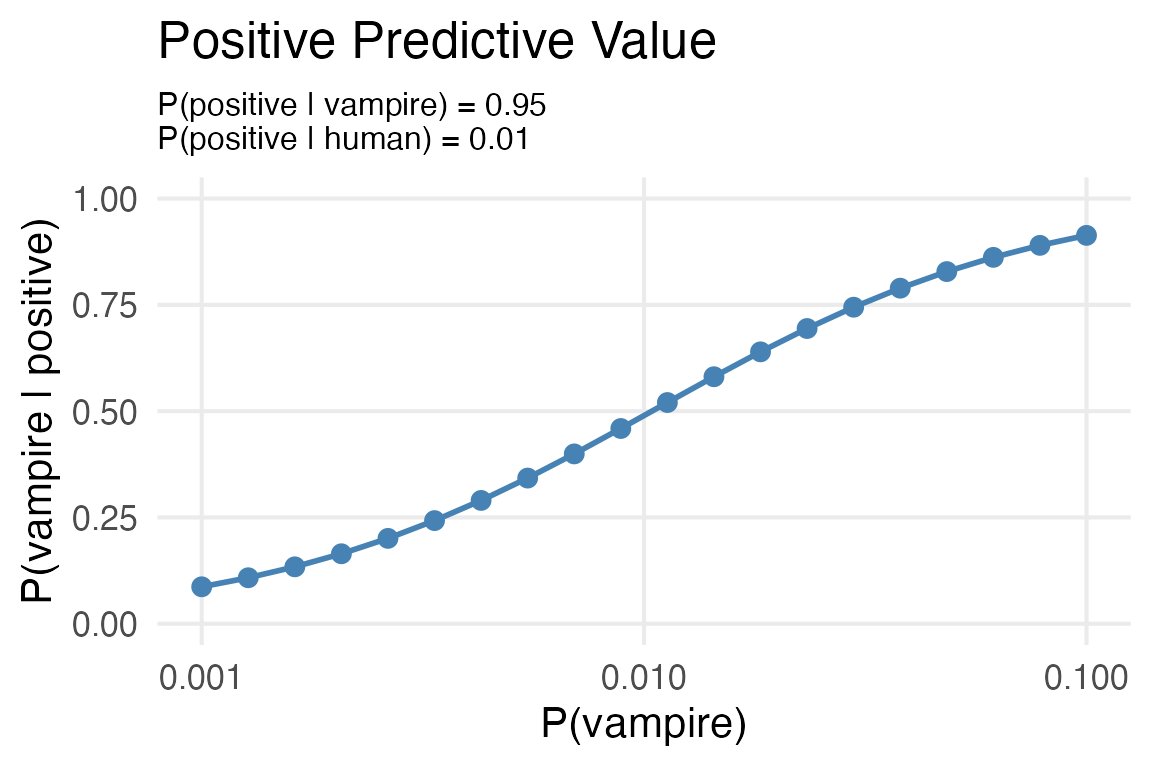

Figure 1: Probability someone is a vampire, given that they tested positive, relative to the base rate of being a vampire

test_metrics |> 
  ggplot(aes(base_rate, p_hum_neg))+
    geom_point(color = "steelblue", 
               size = 3)+
    geom_line(color = "steelblue",
              linewidth = 1)+
    scale_x_log10()+
    labs(x = "P(vampire)",
         y = "P(human | negative)",
         subtitle = "P(positive | vampire) = 0.95\nP(positive | human) = 0.01",
         title = "Negative Predictive Value") +
    theme(plot.subtitle = element_text(size = 12))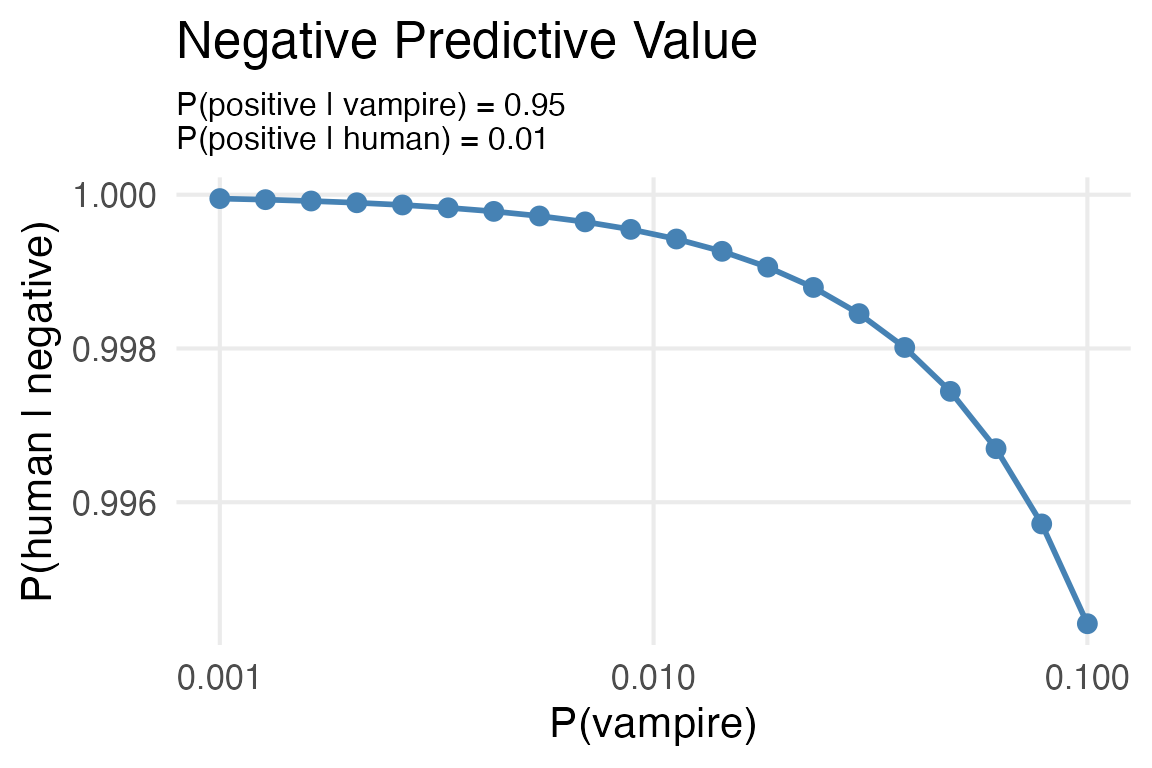

Figure 2: Probability of being a human given a negative test, relative to the base rate of being a vampire.

Tibble grid sampling

Estimating posterior density from grid sampling.

grid <- tibble(
  # The grid
  prob = seq(0.0001, 0.9999, length = 5000), 
  
  # the prior
  prior_unstd = exp(-abs(prob - .5) / .25),
  prior_std = prior_unstd/sum(prior_unstd),
  
  # the data
  data = dbinom(6, size = 9, prob = prob),
  
  # the posterior
  posterior_unstd = prior_std * data,
  posterior = posterior_unstd / sum(posterior_unstd)
)

grid |> 
  ggplot(aes(prob, prior_std))+
    geom_line()+
    labs(y = "prior density",
         title = "Prior") -> 
  prior_plot

grid |> 
  ggplot(aes(prob, data))+
    geom_line()+
    labs(y = "data density",
         title = "Data") -> 
  data_plot

grid |> 
  ggplot(aes(prob, posterior))+
    geom_line() +
    labs(y = "posterior density",
         title = "Posterior") -> 
  posterior_plot

prior_plot | data_plot | posterior_plot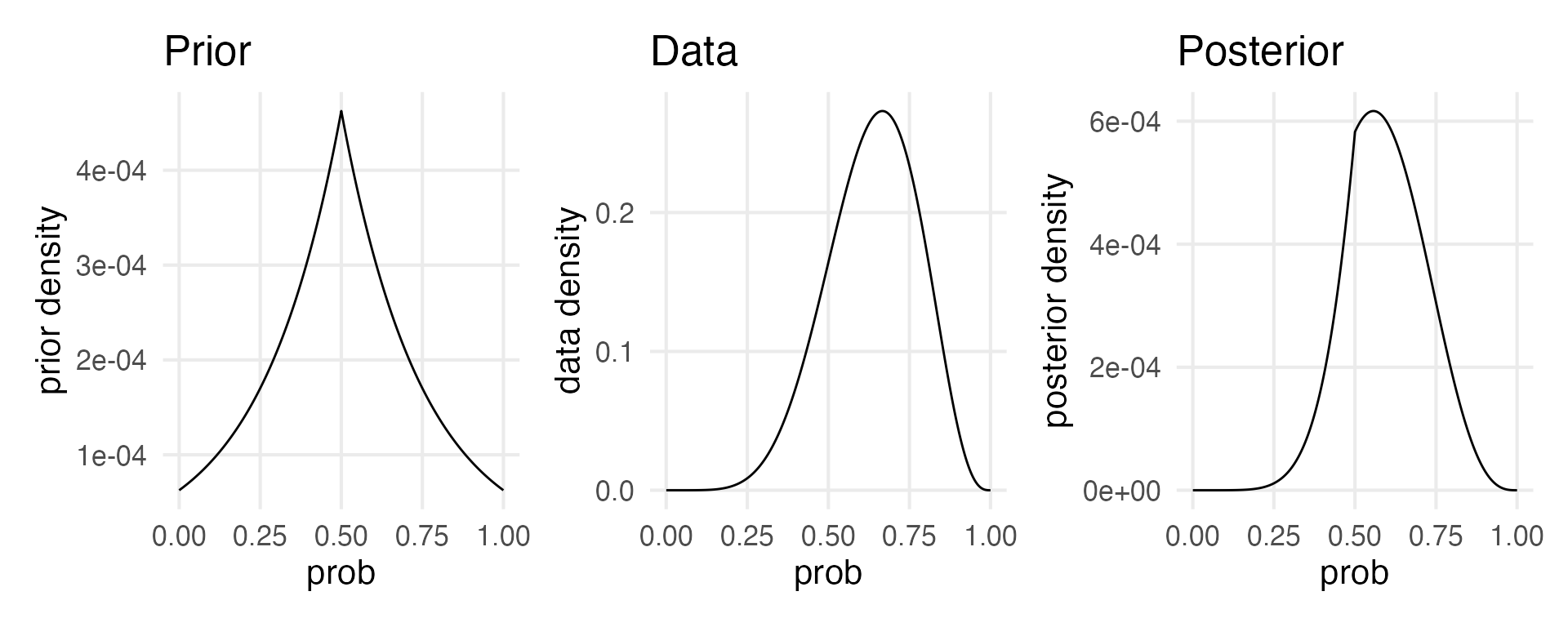

Sampling from the posterior, using sample_n().

grid |> 
  sample_n(size = 1e4, 
           replace = T,
           weight = posterior)->
  posterior_samples

head(posterior_samples)

# A tibble: 6 × 6
   prob prior_unstd prior_std  data posterior_unstd posterior
  <dbl>       <dbl>     <dbl> <dbl>           <dbl>     <dbl>
1 0.703       0.444  0.000205 0.266       0.0000546  0.000419
2 0.694       0.461  0.000213 0.269       0.0000574  0.000441
3 0.670       0.507  0.000234 0.273       0.0000640  0.000491
4 0.559       0.789  0.000365 0.220       0.0000803  0.000616
5 0.620       0.619  0.000286 0.262       0.0000749  0.000575
6 0.632       0.591  0.000273 0.267       0.0000729  0.000559

I’m going to mess around with finessing the visualizations here.

renv::install("tidybayes")

library(tidybayes)

posterior_samples |> 
  pull(prob) |> 
  density() |> 
  tidy() |> 
  rename(prob = x, density = y) ->
  posterior_dens

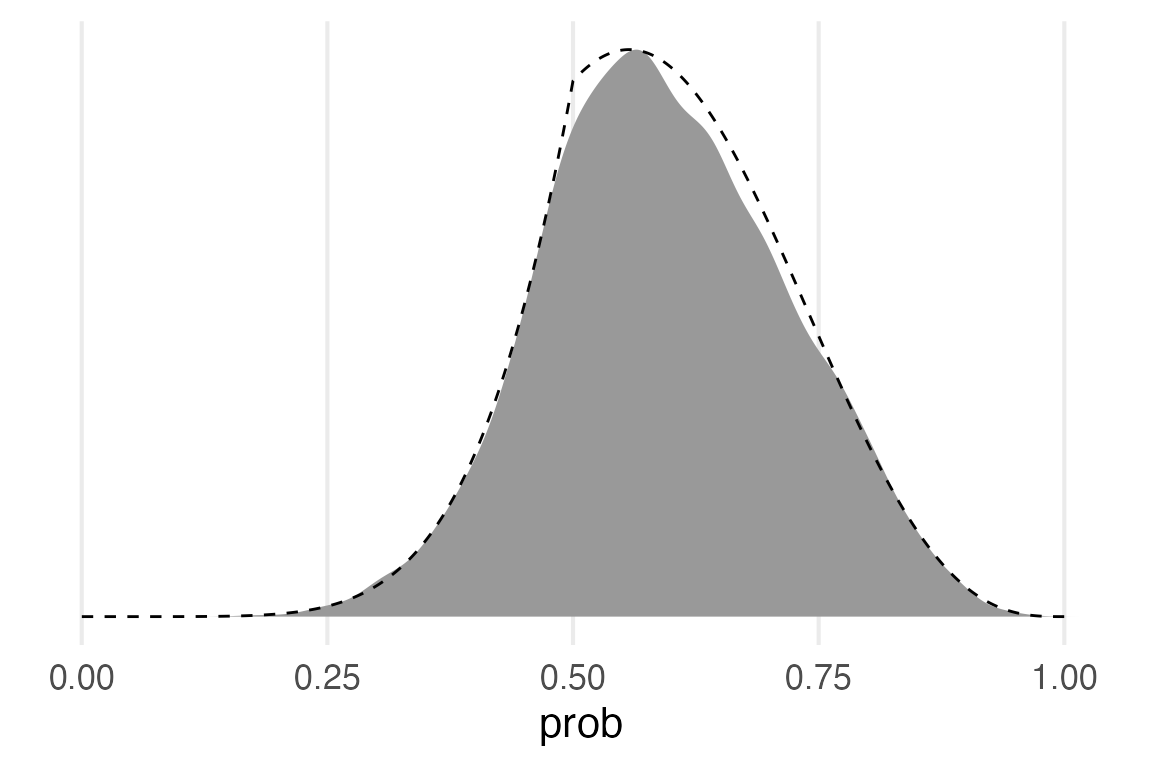
posterior_dens |> 
  ggplot(aes(prob, density/max(density)))+
    geom_area(fill = "grey60")+
    geom_line(aes(y = posterior/max(posterior)),
              linetype = 2,
              data = grid)+
    theme(
      axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      panel.grid.major.y = element_blank()
    )

Figure 4: Comparison of the kernel density estimate vs the actual posterior distribution.

posterior_samples |> 
  median_hdci(prob, .width = c(0.5, 0.95)) ->
  intervals
intervals |> 
  gt() |> 
  fmt_number(decimals = 2)

prob	.lower	.upper	.width	.point	.interval
0.59	0.48	0.65	0.50	median	hdci
0.59	0.37	0.85	0.95	median	hdci

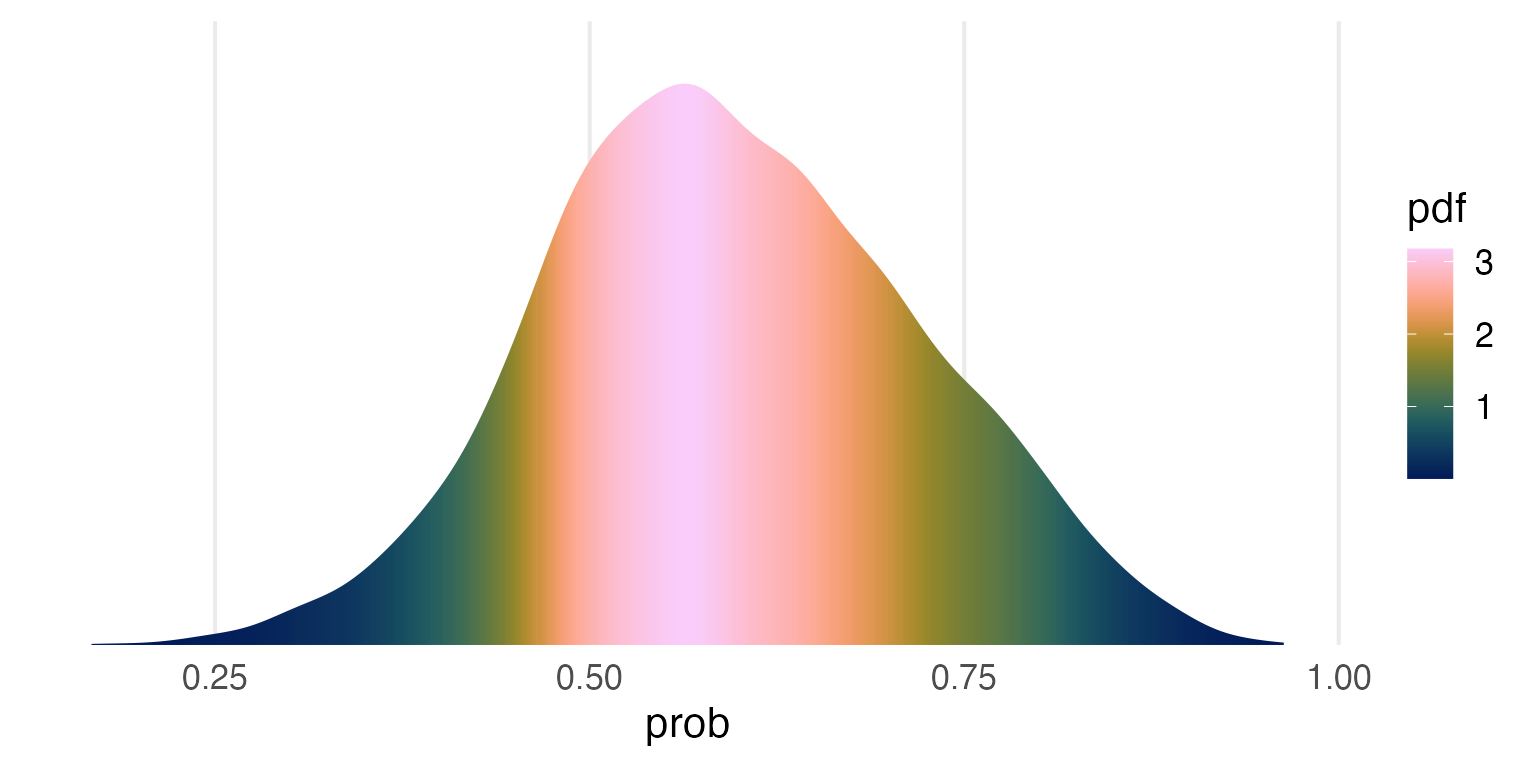
posterior_samples |> 
  ggplot(aes(prob))+
    stat_slab(aes(fill = after_stat(pdf)), 
              fill_type = "gradient")+
    scale_y_continuous(expand = expansion(mult = c(0,0)))+
    khroma::scale_fill_batlow() +
    theme(
      axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      panel.grid.major.y = element_blank()
    )

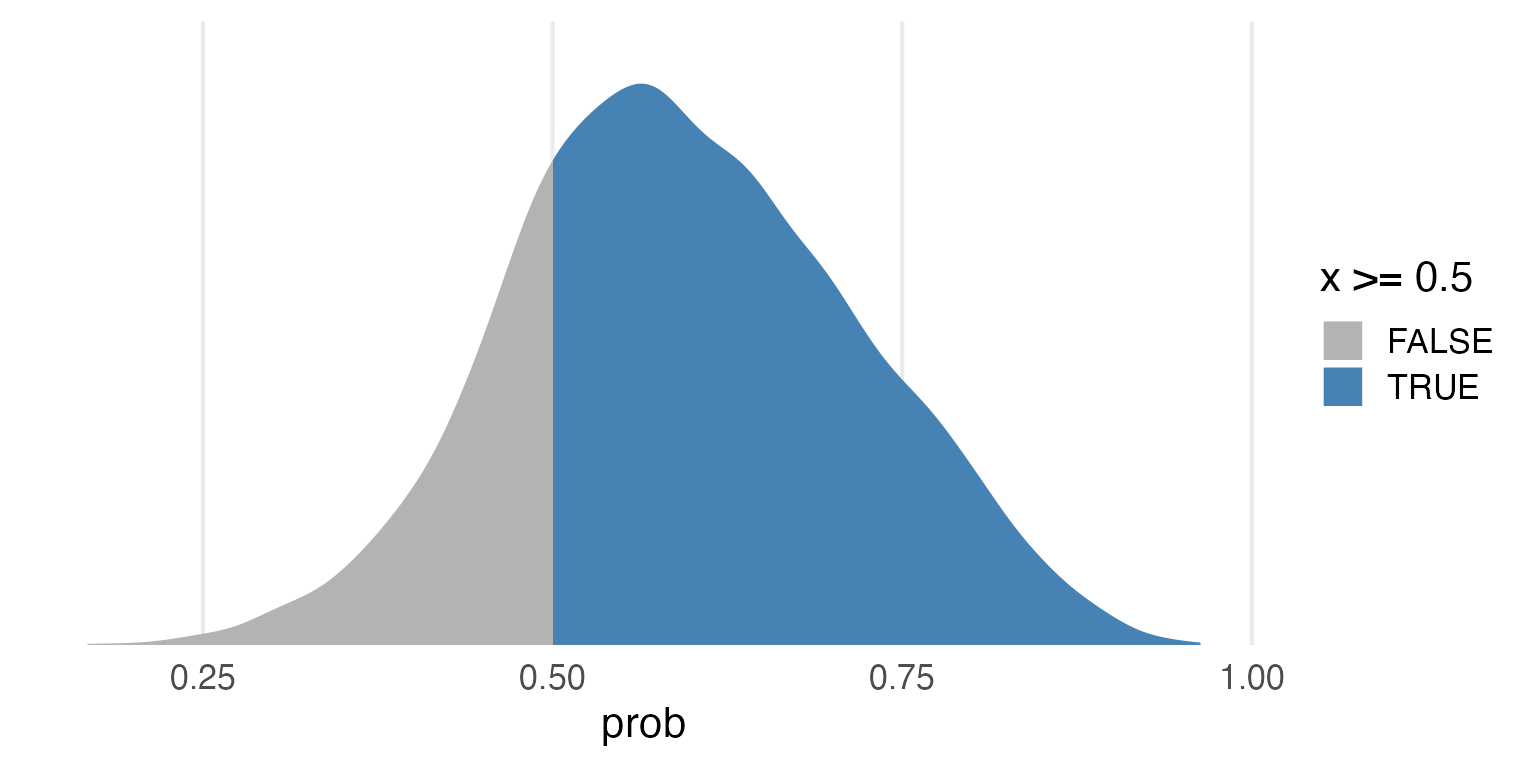
Figure 5: Posterior density, colored according to the probability density function.

posterior_samples |> 
  ggplot(aes(prob))+
    stat_slab(
      aes(fill = after_stat(x >= 0.5)),
      fill_type = "gradient"
    ) +
    scale_fill_manual(
      values = c(
        "grey70",
        "steelblue"
      )
    )+
   scale_y_continuous(expand = expansion(mult = c(0,0)))+
   theme(
      axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      panel.grid.major.y = element_blank()
    )

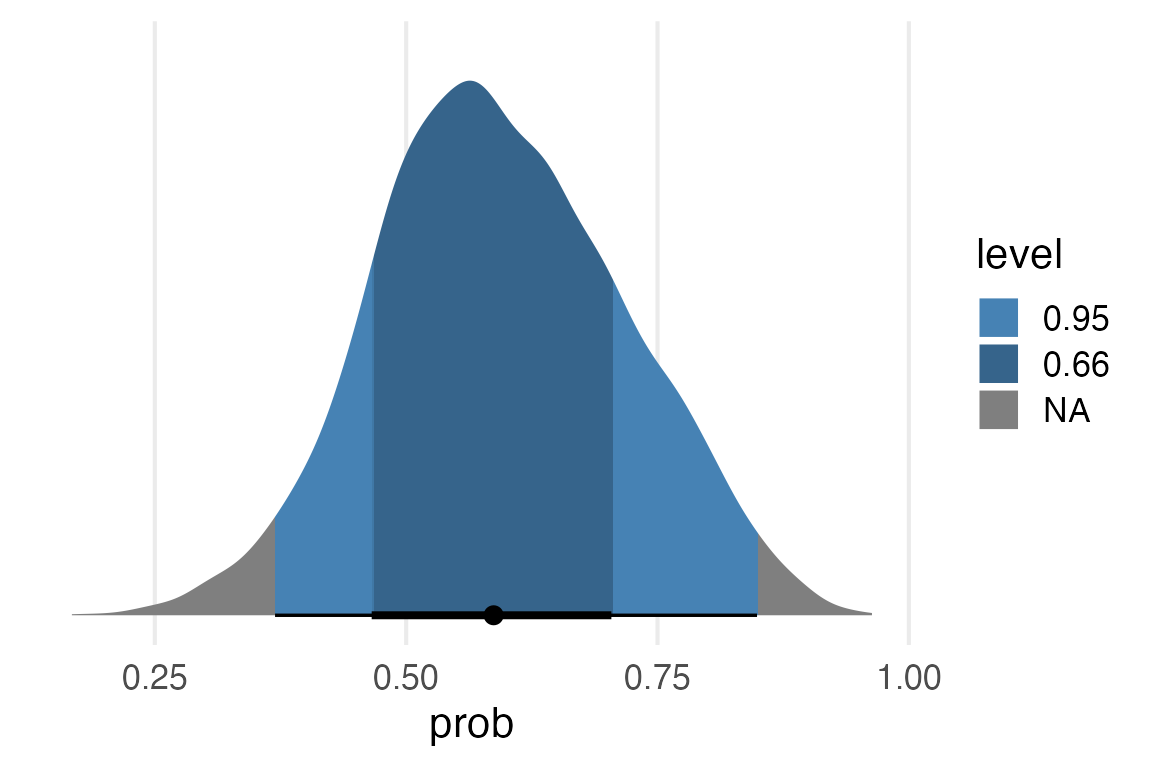
Figure 6: The posterior density colored according to a critical value (0.5)

posterior_samples |> 
  ggplot(aes(prob))+
    stat_halfeye(
      aes(fill = after_stat(level)),
      fill_type = "gradient",
      point_interval = "median_hdi"
    ) +
   scale_y_continuous(expand = expansion(mult = c(0.05,0)))+
   scale_fill_manual(
     values = c("steelblue", "steelblue4")
   )+
   theme(
      axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      panel.grid.major.y = element_blank()
    )

Figure 7: Posterior samples, colored by their highest density interval levels.

Can I get the plot into a {gt} table? I thin I’ll need to map over the widths? I’m going off of this gt help page: https://gt.rstudio.com/reference/ggplot_image.html. Let me get the plot right first.

posterior_samples |> 
  ggplot(aes(prob))+
    stat_slab(
      aes(fill = after_stat(level)),
      .width = 0.66,
      fill_type = "gradient",
      point_interval = "median_hdci"
    ) +
    stat_slab(
      fill = NA,
      color = "black"
    )+
    scale_x_continuous(
      limits = c(0,1),
      expand = expansion(mult = c(0,0))
    )+
    scale_y_continuous(
      expand = expansion(mult = c(0,0))
    )+
    scale_fill_manual(values = "steelblue", 
                      guide = "none")+
    theme_void()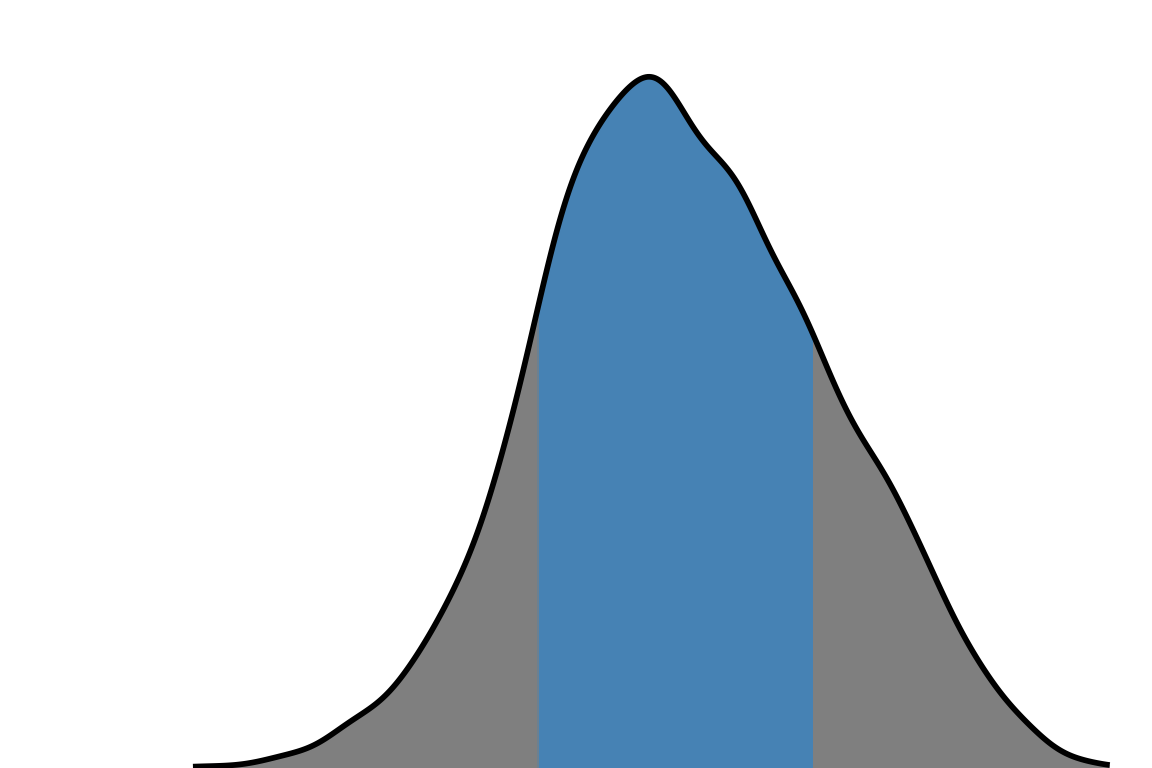

make_table_plot <- function(.width, data) {
  ggplot(data, aes(prob))+
    stat_slab(
      aes(fill = after_stat(level)),
      .width = .width,
      point_interval = "median_hdci"
    ) +
    stat_slab(
      fill = NA,
      color = "black"
    )+
    scale_x_continuous(
      limits = c(0,1),
      expand = expansion(mult = c(0,0))
    )+
    scale_y_continuous(
      expand = expansion(mult = c(0,0))
    )+
    scale_fill_manual(values = "steelblue", 
                      guide = "none")+
    theme_void()
}

Map that function over the intervals table I made before.

intervals |> 
  mutate(
    ggplot = map(.width, ~make_table_plot(.x, posterior_samples)),
    
    ## adding an empty column
    dist = NA
  ) -> to_tibble

to_tibble |> 
  select(-ggplot) |> 
  gt() |> 
  text_transform(
    locations = cells_body(columns = dist),
    fn = \(x) map(to_tibble$ggplot, ggplot_image, aspect_ratio = 2)
  )

prob	.lower	.upper	.width	.point	.interval	dist
0.587	0.4815000	0.6503000	0.50	median	hdci
0.587	0.3695874	0.8489874	0.95	median	hdci

I’d like more control over how the image appears in the table. Looks like I’ll have to ggsave, and then embed.

make_custom_table_plot <- function(p){
  filename <- tempfile(fileext = ".png")
  ggsave(plot = p, 
         filename = filename, 
         device = ragg::agg_png, 
         res = 100, 
         width =1.5,
         height = 0.75)
  local_image(filename=filename)
}

to_tibble |> 
  select(-ggplot) |> 
  gt() |> 
  text_transform(
    locations = cells_body(columns = vars(dist)),
    fn = \(x) map(to_tibble$ggplot, make_custom_table_plot)
  )

prob	.lower	.upper	.width	.point	.interval	dist
0.587	0.4815000	0.6503000	0.50	median	hdci
0.587	0.3695874	0.8489874	0.95	median	hdci

There we go!

Turns out this local_image() thing doesn’t play nice with conversion to pdf (😕).

BRMS

library(brms)

tibble(
  water = 6,
  samples = 9
)-> 
  water_to_model

water_form <- bf(
   water | trials(samples) ~ 1,
   family = binomial(link = "identity")
)

brm(
  water | trials(samples) ~ 1,
  data = water_to_model,
  family = binomial(link = "identity"),
  prior(beta(1, 1), class = Intercept, ub = 1, lb = 0),
  file_refit = "on_change",
  file = "water_fit.rds"
) ->
  water_model

water_model

 Family: binomial 
  Links: mu = identity 
Formula: water | trials(samples) ~ 1 
   Data: water_to_model (Number of observations: 1) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept     0.64      0.14     0.35     0.88 1.00     1598     1945

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

library(gtsummary)

water_model |> 
  gtsummary::tbl_regression(intercept = T)

Characteristic	Beta	95% CI¹
(Intercept)	0.64	0.35, 0.88
¹ CI = Credible Interval

Let’s do this again.

water_model |> 
  get_variables()

[1] "b_Intercept"   "lprior"        "lp__"          "accept_stat__"
[5] "stepsize__"    "treedepth__"   "n_leapfrog__"  "divergent__"  
[9] "energy__"

water_model |> 
  gather_draws(b_Intercept)->
  model_draws

model_draws |> 
  head() |> 
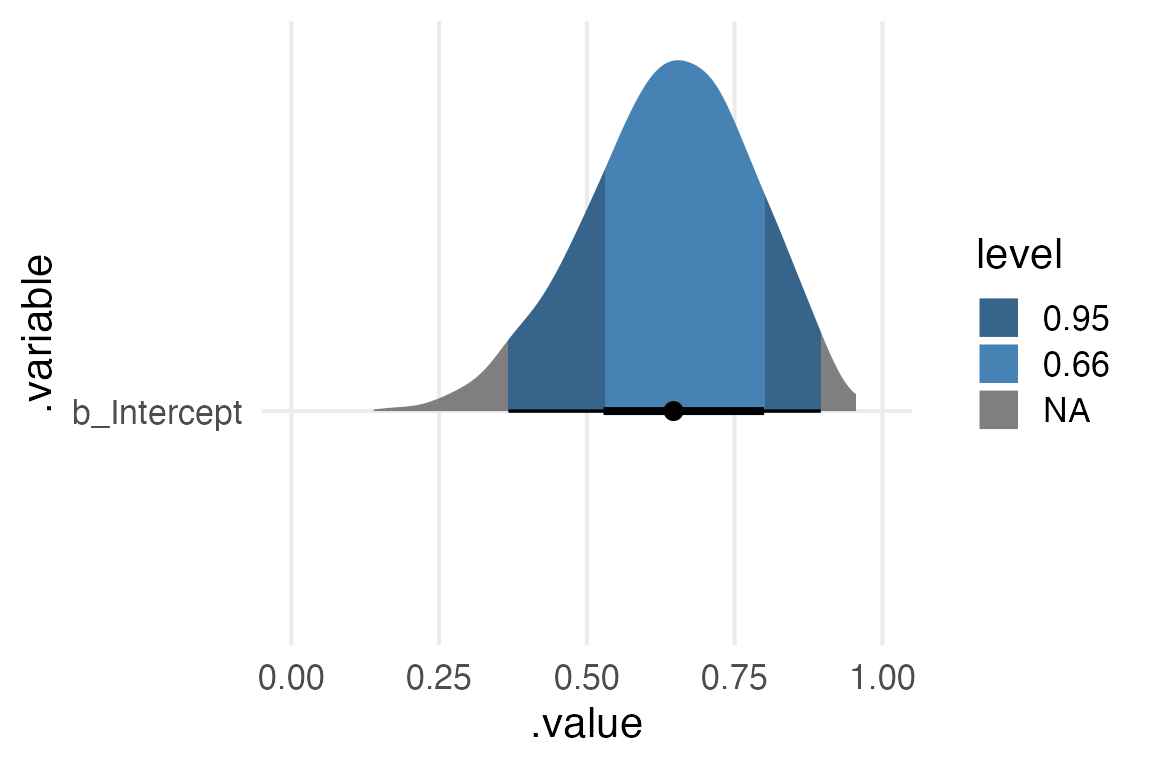
  rmarkdown::paged_table()

model_draws |> 
  ggplot(aes(.value, .variable)) + 
    stat_halfeye(
      point_interval = median_hdi,
      aes(fill = after_stat(level)),
      fill_type = "gradient"
    ) +
    xlim(0,1)+
    scale_fill_manual(
      values = c("steelblue4", "steelblue"),
    )