Random Effects and Overdispersion

Today in my stats class, my students saw me realize, in real-time, that you can include random intercepts in poisson models that you couldn’t in ordinary gaussian models, and this might be a nicer way to deal with overdispersion than moving to a negative binomial model.

source(here::here("_defaults.R"))

library(tidyverse)
library(brms)
library(distributional)
library(ggdist)
library(palmerpenguins)
library(gt)
library(marginaleffects)

Impossible ranefs

Let’s start off with the Palmer Penguin data

penguins |> 
  gt_preview()

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex	year
1	Adelie	Torgersen	39.1	18.7	181	3750	male	2007
2	Adelie	Torgersen	39.5	17.4	186	3800	female	2007
3	Adelie	Torgersen	40.3	18.0	195	3250	female	2007
4	Adelie	Torgersen	NA	NA	NA	NA	NA	2007
5	Adelie	Torgersen	36.7	19.3	193	3450	female	2007
6..343
344	Chinstrap	Dream	50.2	18.7	198	3775	female	2009

As far as I know, no individual penguin is represented in the data twice. So let’s add an individual column that’s the same as the row number.

penguins |> 
  mutate(
    individual = row_number(),
    .before = 1
  )->
  penguins

If we try to fit an intercept only model for, say, bill length, and include a random intercept for individual, things are going to get wonky.

peng_remod <- brm(
  bill_length_mm ~ 1 + (1|individual),
  data = penguins,
  backend = "cmdstanr",
  file = "peng_re"
)

peng_remod

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: bill_length_mm ~ 1 + (1 | individual) 
   Data: penguins (Number of observations: 342) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Multilevel Hyperparameters:
~individual (Number of levels: 342) 
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept)     2.03      1.29     0.08     4.82 1.14       25       18

Regression Coefficients:
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept    43.92      0.29    43.38    44.49 1.01      502     1634

Further Distributional Parameters:
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     4.87      0.75     2.58     5.74 1.15       22       20

Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Nothing’s converged, everything’s divergent, what’s going on here!

Well, if we think about how the model is defined, and the structure of the data, it makes a bit more sense. We’re telling the model to estimate \(\mu_i\) this way

\[ \mu_i = \beta_0 + \gamma_i \]

Where \(\gamma_i\) is a random intercept by individual. \(\gamma_i\) is meant to be sampled from a normal distribution like:

\[ \gamma_i \sim \mathcal{N}(0, \sigma_{\gamma}) \]

Then, we’re saying the data is sampled from a normal distribution like this

\[ y_i \sim \mathcal{N}(\mu_i, \sigma) \]

The problem is that because every row is one individual, the sampling statement for \(\gamma_i\) is basically a description of the residual error, and \(\sigma_{\gamma}\) would wind up being equivalent to the standard deviation of the residuals. But that’s also what \(\sigma\) in the sampling statement for \(y_i\) is supposed to be.

One way to think about what’s happened is we’ve created an identifiability problem, trying to account for the residual error with two different parameters. Another way to think about is that the individual level variation around the population mean that we wanted to capture with (1|individual) was already being captured by the residual error.

Poisson Models & Overdispersion

I’d like to thank Andrew Heiss for having his course materials online, as they helped inform my thinking on this. The data set below has a count of how many times people said “like” in interviews.

like_df <- read_csv(
  "https://lin611-2024.github.io/notes/meetings/data/like.csv"
) |> 
  mutate(
    dob_g = (dob-1985)/20,
    .after = dob
  )

like_df |> 
  gt_preview()

	id	filler	n	dob	dob_g	total_words
1	s_001	LIKE	79	1953	-1.60	3524
2	s_002	LIKE	457	1990	0.25	4842
3	s_003	LIKE	14	1914	-3.55	2148
4	s_004	LIKE	17	1937	-2.40	1799
5	s_005	LIKE	11	1904	-4.05	2457
6..352
353	s_353	LIKE	20	1963	-1.10	2295

I’ll first try fitting this with a standard poisson model.

\[ \log(\lambda_i) = \beta_0 + \beta_1\text{dob} + \log(\text{total.words)} \]

\[ y_i \sim \text{Pois}(\lambda_i) \]

like_pois <- brm(
  n ~ dob_g + offset(log(total_words)),
  family = poisson(),
  data = like_df,
  backend = "cmdstanr",
  file = "like_pois"
)

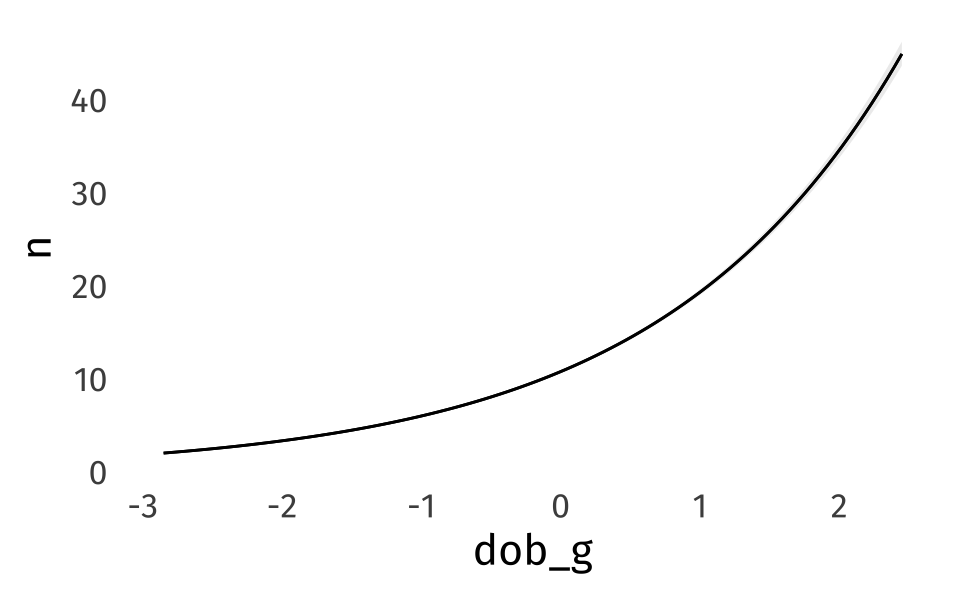
plot_predictions(
  like_pois,
  newdata = datagrid(
    dob_g = \(x) seq(min(x), max(x), length = 100),
    total_words = 1000
  ),
  by = "dob_g"
)

If we look at the posterior predictive check, we can see that we’ve got some overdispersion.

pp_check(like_pois)+
  scale_x_log10()

The poisson distribution is assuming a narrower range of “like” counts than the data has.

predictions(
  like_pois, 
  newdata = datagrid(
    dob_g = \(x) seq(min(x), max(x), length = 100),
    total_words = 1000
  )
) |> 
  as_tibble() |> 
  mutate(
    like_dist = dist_poisson(estimate)
  ) ->
  pois_pred

pois_pred |> 
  ggplot(
    aes(
      dob_g
    )
  )+
  stat_lineribbon(
    aes(
      ydist = like_dist
    )
  )+
  geom_point(
    data = like_df,
    aes(
      y = (n/total_words)*1000
    ),
    color = "grey",
    alpha = 0.6
  )+
  labs(
    y = "likes per 1000"
  )

It’s too bad we can’t add a random effect by speaker, but just like the penguins, we’ve only got one row per individual…

But wait! Look at the \(y_i\) sampling statement again!

\[ y_i \sim \text{Pois}(\lambda_i) \]

There’s no observation-level variance term in a poisson distribution. Its mean and variance are the same,

pois_ex <- dist_poisson(1:10)

mean(pois_ex)

 [1]  1  2  3  4  5  6  7  8  9 10

variance(pois_ex)

 [1]  1  2  3  4  5  6  7  8  9 10

So, adding a row-level random variable wouldn’t introduce the same non-identifiability issue.

\[ \log(\lambda_i) = \beta_0 + \beta_i\text{dob} + \gamma_i \]

\[ \gamma_i\sim\mathcal{N}(0, \sigma) \]

\[ y_i \sim \text{Pois}(\lambda_i) \]

like_repois <- brm(
  n ~ dob_g + (1|id) + offset(log(total_words)),
  family = poisson(),
  data = like_df,
  backend = "cmdstanr",
  file = "like_repois"
)

like_repois

 Family: poisson 
  Links: mu = log 
Formula: n ~ dob_g + (1 | id) + offset(log(total_words)) 
   Data: like_df (Number of observations: 353) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Multilevel Hyperparameters:
~id (Number of levels: 353) 
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept)     0.57      0.03     0.52     0.62 1.01      538     1157

Regression Coefficients:
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept    -3.93      0.06    -4.06    -3.81 1.01      409      909
dob_g         0.43      0.03     0.37     0.48 1.01      472     1059

Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

We are all converged, with no divergent transitions.

plot_predictions(
  like_repois,
  newdata = datagrid(
    dob_g = \(x) seq(min(x), max(x), length = 100),
    total_words = 1000
  ),
  re_formula = NA,
  by = "dob_g"
) +
  geom_point(
    data = like_df,
    aes(
      x = dob_g,
      y = (n/total_words)*1000
    ),
    alpha = 0.2,
    color = "#EE6677"
  )+
  labs(
    y = "like per 1000"
  )

And the posterior predictive check looks a lot better.

pp_check(like_repois)+
  scale_x_log10()

Negative Binomial?

The stats notes I linked to above turned to a negative binomial model to use in a case of overdispersion like this. I’m not quite in a place to evaluate the pros and cons of the negative binomial vs this random effects approach in general. But for this case I like the random effects better because

1. It lines up with how I think about this data as having a population level trend, with individual divergences off of it.
2. It’s easier for me to explain and understand than whatever the shape parameter is for the negative binomial.