Rolling for Damage with the Central Limit Theorem

I’ve been playing a lot of Baldur’s Gate 3 lately. My party has gotten to max level, and we’re running around, casting spells and taking names.

One of the spells my wizard has is called Disintegrate, which gets summarized like this

Disintegrate

Shoot a thin green ray from your finger. If the spell reduces the target to 0 hit points, it disintegrates into a crumbly ash.

Damage

🎲 10d6 + 40 (50~100)

The line of information under “Damage” means that to calculate how much damage you do when you cast the spell, you need to roll 10 6-sided dice (“d6”), then add 40. The “(50~100)” part summarizes the worst vs best outcomes.

Best and worst

Worst

: You roll 10 d6, and they all come up 1: 1,1,1,1,1,1,1,1,1,1. This sums to 10, then you add 40 to get a total of 50.

Best

You roll 10 d6, and they all come up 6: 6,6,6,6,6,6,6,6,6,6. This sums up to 60, then you add 40 to get a total of 100.

If you just glance at the description saying that the spell will do between 50 and 100 damage, you might think that you’re equally likely to roll any amount of damage between these two values.

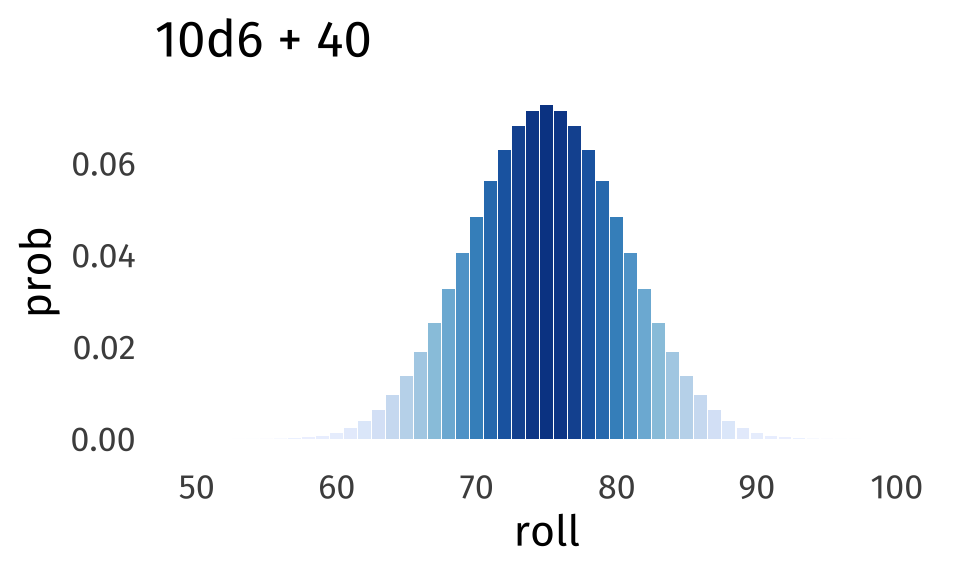
But, as you play, you’ll find that hitting something right in the middle, like 75, is very likely, and that hitting either 50 or 100 is vanishingly rare. The distribution of rolls wind up looking like this:

In fact, 95% of the rolls are going to be between 64 and 86. The rest of this post is about these two questions:

1. Why is that?
2. Is that a normal distribution?

Why is that?

1d6

We should start things off easy, and look at what happens when we roll 1d6. As long as the die is fair, any value between 1 and 6 is possible. And for each value between 1 and 6, there’s only 1 possible way to get that value.

total	rolls	n
1	1	1
2	2	1
3	3	1
4	4	1
5	5	1
6	6	1

2d6

Things are more complicated when we start rolling 2d6 and summing them together. Let’s name each of our die “Alpha” and “Beta” to keep them straight.

There’s only one way for us to get a total roll of 2: both Alpha and Beta need to come up 1. Same thing for a total roll of 12: both Alpha and Beta need to come up 6.

But to roll a value of 3, there are two ways.

• Alpha rolls 1, and Beta rolls 2.

• Alpha rolls 2, and Beta rolls 1.

If we expand this out to look at all possible values between 2 and 12, we’ll find that there’s six unique ways to roll 7, with each value above and below having fewer unique ways.

total	rolls	n
2	1 1	1
3	1 2; 2 1	2
4	1 3; 2 2; 3 1	3
5	1 4; 2 3; 3 2; 4 1	4
6	1 5; 2 4; 3 3; 4 2; 5 1	5
7	1 6; 2 5; 3 4; 4 3; 5 2; 6 1	6
8	2 6; 3 5; 4 4; 5 3; 6 2	5
9	3 6; 4 5; 5 4; 6 3	4
10	4 6; 5 5; 6 4	3
11	5 6; 6 5	2
12	6 6	1

There’s just more different ways for a very large roll on Alpha to get balanced out by a smaller roll on Beta.

10d6

If we expand this out to the 10d6 situation, where there’s only one way to roll 10 (all six die roll 1), there are 4,395,456 different ways to roll 35. The massively larger number of ways to get 35 results in it showing up that much more often than 10 (or 60).

Is that a Normal Distribution?

Yes, or, at least it’s approximating one. This is, in fact, a demonstration of the “Central Limit Theorem”. The Central Limit Theorem states that if we take a bunch of samples from a single distribution and average them together, and we keep doing that, the distribution of the averages will approach a normal distribution.

An average is the sum of a list of numbers, divided by now many numbers there are. When we roll for damage in D&D, we just do the summing part, but the result is still going to approximate the Normal Distribution.

Unfair dice

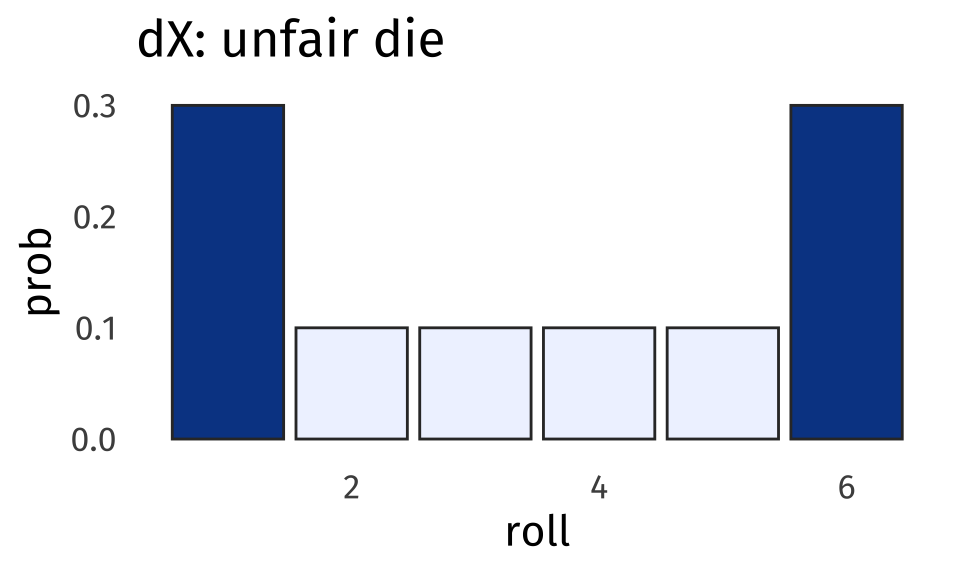
The nifty thing about the Central Limit Theorem is that it works no matter what the shape of the original distribution was. Let’s say we had a 10 sided die, but 3 of the sides have “1” painted, 3 of the sides have “6” painted on them, and the rest have 2 through 5. With this die, we’re a lot more likely to roll a 1 or a 6.

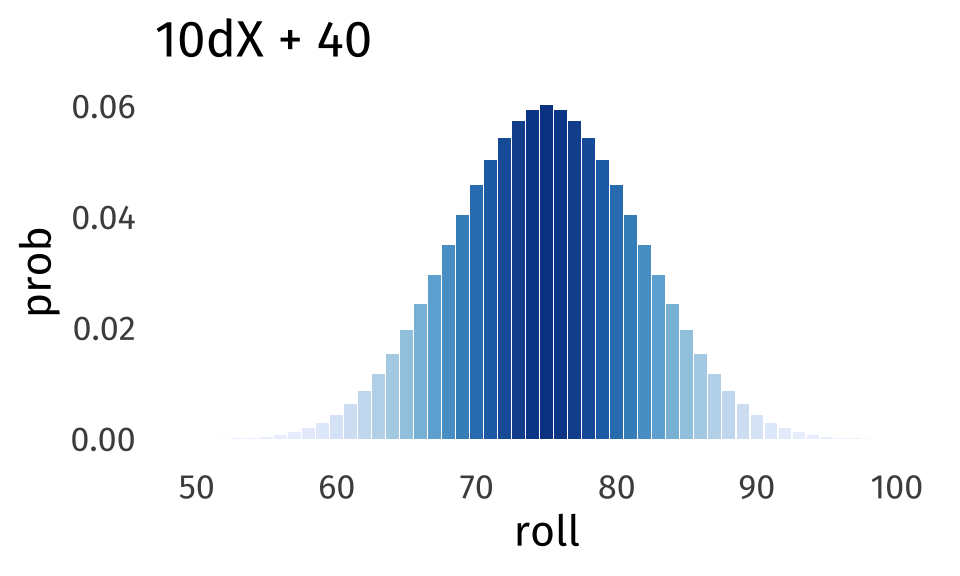
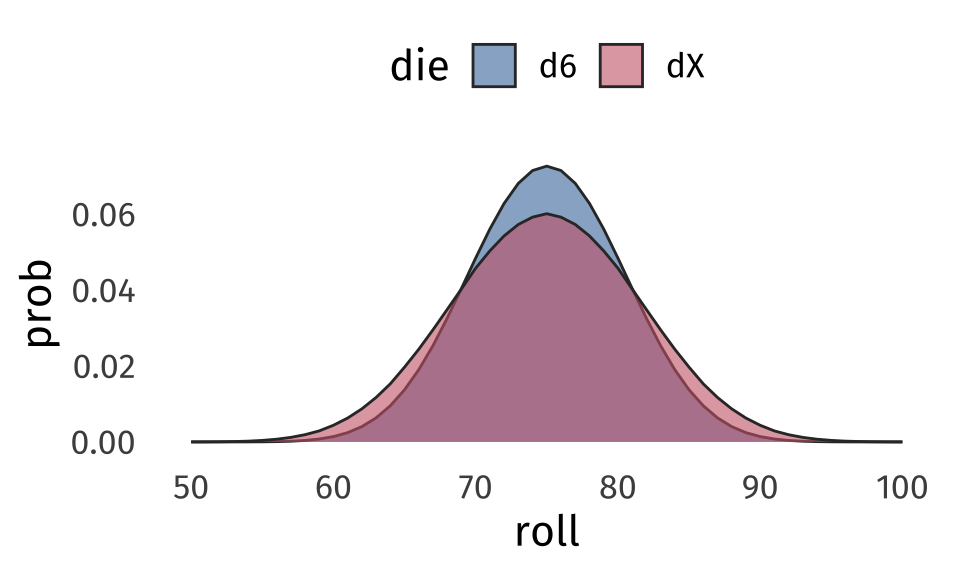
If we used this unfair die, to roll damage for the Disintegrate spell, how will that affect the outcome?

It might be hard to see the difference, but this unfair die is slightly more spread out than the fair d6

But, even though it’s more spread out, it’s still approximating a normal distribution!