Generalized Linear Models

Setup

library(tidyverse)
library(lme4)
library(broom.mixed)
library(marginaleffects)

Logistic Regression (a.k.a. binary data)

um_dat <- read_tsv("https://bit.ly/3JdeSbx")
demog <- read_csv("https://bit.ly/3wOfcGx")

um_dat <- um_dat |> 
  left_join(demog)

Preparing for modelling

um_dat |> 
  # only looking at UM and UH
  filter(
    word %in% c("UM", "UH"),
    is.finite(dob)
  )  |> 
  mutate(
    # 0 if UH, 1 if UM
    um_binary = (word == "UM") * 1,
    # centering and scaling dob
    dob_c = dob - 1970,
    dob_s = dob_c / 25,
    # setting gender levels
    gender = fct_relevel(gender, "f")
  ) -> um_to_model

Modelling

um_model <- glmer(um_binary ~ dob_s * gender + (1 | idstring),
                  data = um_to_model,
                  family = binomial)

tidy(um_model) |> 
  rmarkdown::paged_table()

Predictions

Just to get a sense of the range of dob_s

summary(um_to_model$dob_s)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 -3.240  -1.760  -1.040  -1.061  -0.440   1.120 

predictions(
  um_model,
  newdata = datagrid(
    dob_s = seq(-3, 1, length = 100),
    gender = c("f", "m")
  ),
  type = "response",
  re.form = NA
) |> 
  as_tibble() ->
  um_prob_pred

um_prob_pred |> 
  mutate(dob = (dob_s * 25) + 1970) |>
  ggplot(aes(dob, estimate, color = gender, fill = gender))+
    geom_ribbon(
      aes(ymin = conf.low, ymax = conf.high),
      alpha = 0.3
    )+
    geom_line()+
    scale_color_brewer(palette = "Dark2")+
    scale_fill_brewer(palette = "Dark2")+
    theme_bw()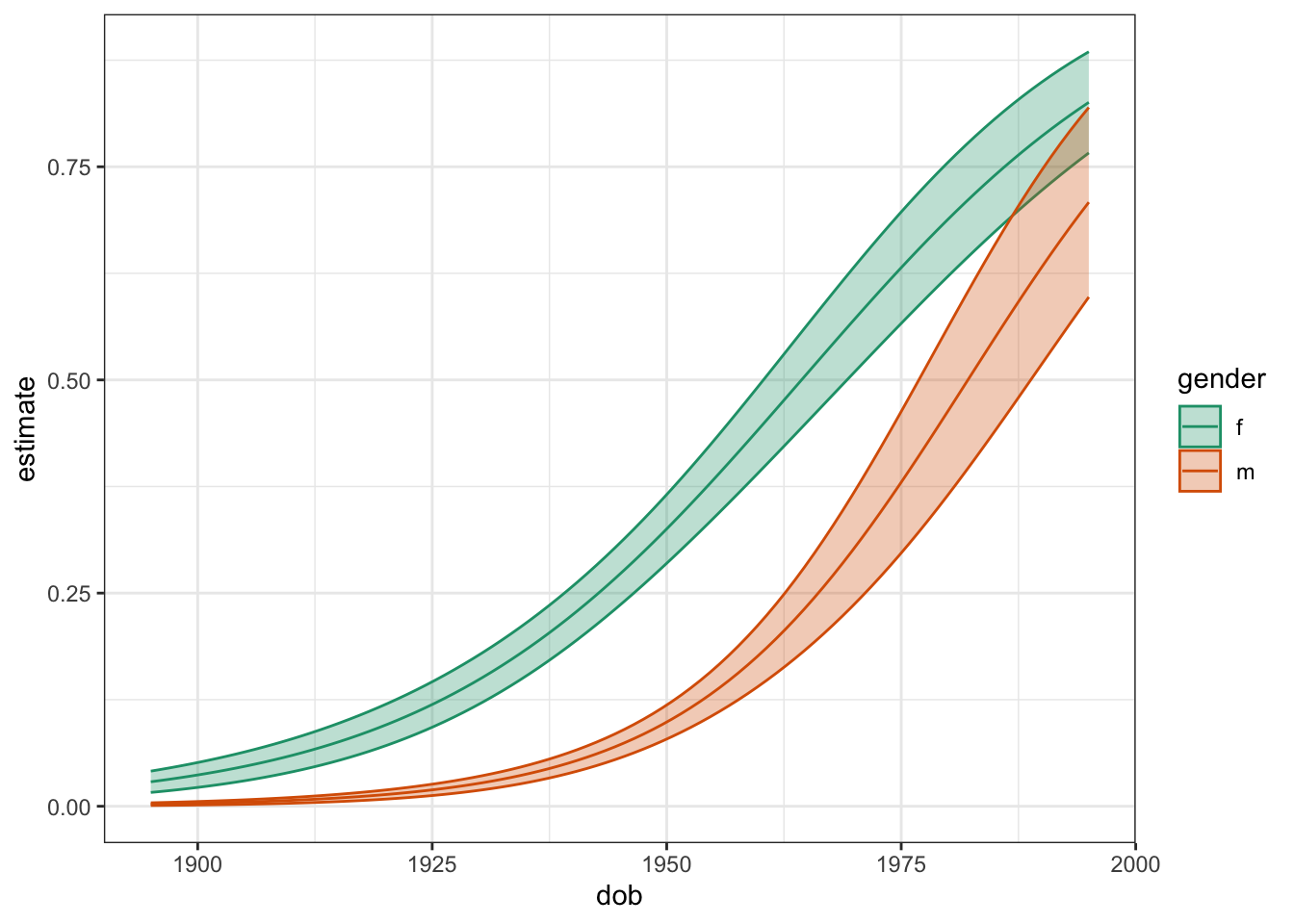

Poisson (or Count)

um_dat |> 
  summarise(
    .by = c(idstring, age, gender, nwords),
    total_fp = n(),
  )->
  fp_count

fp_count |> 
  mutate(
    age_c = age - 40,
    age_s = age_c/10,
    gender = fct_relevel(gender, "m")
  ) ->
  fp_to_model

Modelling

fp_mod <- glmer(total_fp ~ age_s * gender + offset(log(nwords)) + (1|idstring),
                data = fp_to_model,
                family = poisson)

tidy(fp_mod)

# A tibble: 5 × 7
  effect   group    term            estimate std.error statistic    p.value
  <chr>    <chr>    <chr>              <dbl>     <dbl>     <dbl>      <dbl>
1 fixed    <NA>     (Intercept)      -4.22      0.0524    -80.4   0        
2 fixed    <NA>     age_s             0.106     0.0259      4.11  0.0000400
3 fixed    <NA>     genderf          -0.0795    0.0699     -1.14  0.255    
4 fixed    <NA>     age_s:genderf    -0.0476    0.0334     -1.43  0.154    
5 ran_pars idstring sd__(Intercept)   0.662    NA          NA    NA        

Predictions

summary(fp_to_model$nwords)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    274    1928    2725    3583    4376   20489 

predictions(
  fp_mod,
  newdata = datagrid(
    age_s = seq(-2, 5, length = 100),
    gender = c("f", "m"),
    nwords = 1000
  ),
  re.form = NA,
  type = "response"
) |>
  as_tibble()->
  fp_pred

fp_pred |> 
  mutate(age = (age_s * 10) + 40) |>
  ggplot(aes(age, estimate, color = gender, fill = gender))+
    geom_ribbon(aes(ymin = conf.low, ymax = conf.high),
                alpha = 0.3)+
    geom_line()+
    scale_color_brewer(palette = "Dark2")+
    scale_fill_brewer(palette = "Dark2")+
    labs(y = "filled pauses per 1,000 words")+
    theme_bw()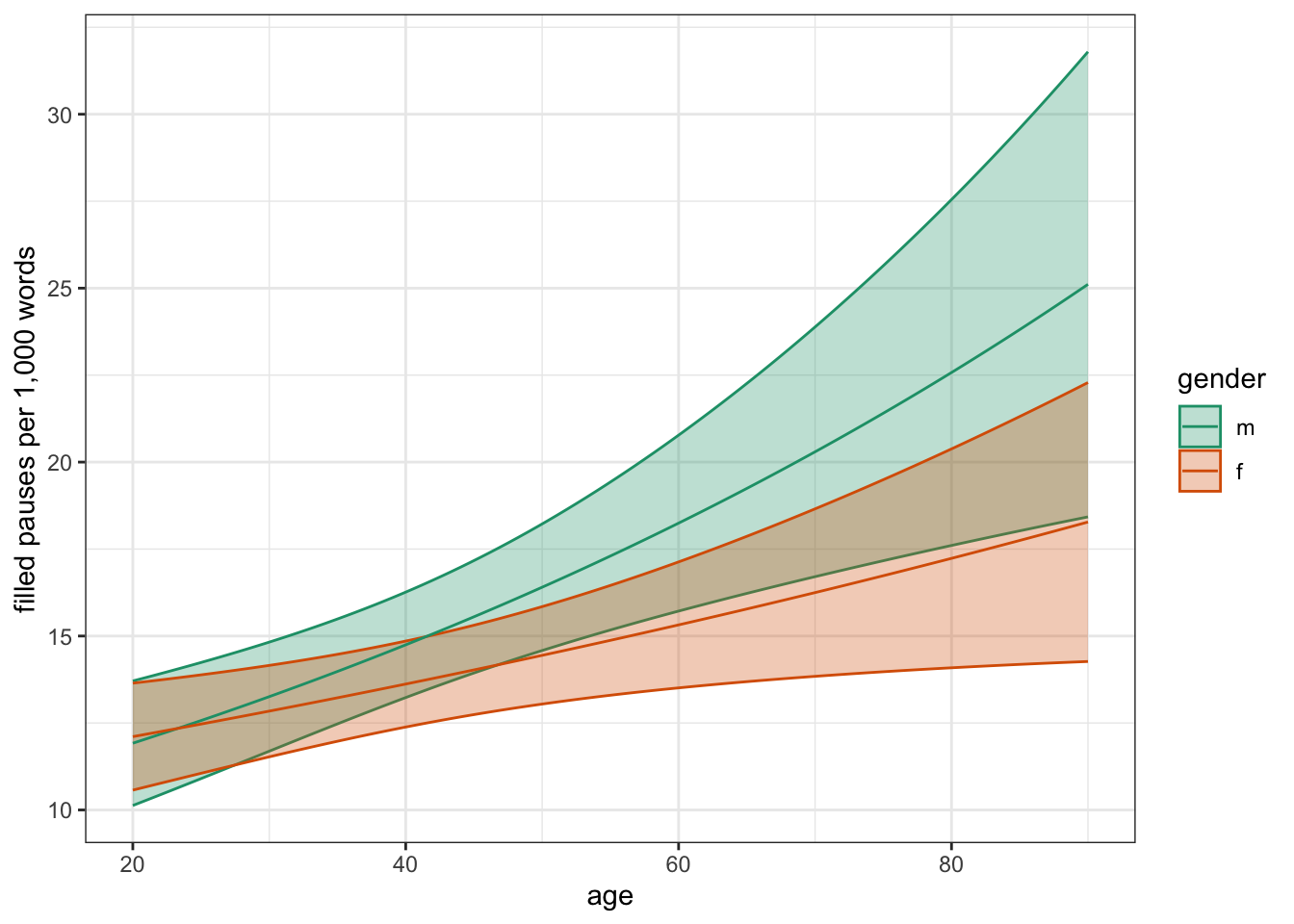

Reuse